12.2 Dijkstrův algoritmus

Hledání nejkratších cest

Fakt (bez důkazu)

Problém nalezení délky nejkratší cesty mezi dvěma vrcholy pro graf ohodnocený obecnými (tedy i zápornými) délkami je NP-těžký – proto pro něj neočekáváme existenci efektivního algoritmu.

Pro některá speciální ohodnocení grafu efektivní algoritmy existují. Dva nejpoužívanější jsou:
- Dijkstrův, který předpokládá kladné délky hran (případně nezáporné).
- Bellmanův-Fordův, který připouští záporné délky, ale předpokládá neexistenci záporných cyklů v grafu.

Úprava BFS pro přirozené váhy

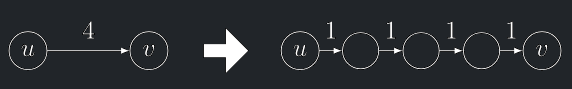
Každou hranu "podrozdělíme" – nahradíme ji cestou tvořenou tolika jednotkovými hranami, kolik činila délka hrany. Image title

Tím vznikne neohodneconý graf, ve kterém lze použít BFS pro hledání nejkratších cest.

Tento algoritmus je funkční, ale neefektivní
- Označíme-li L maximální délku hrany, podrozdělením vznikne \(O(L · m)\) nových vrcholů a hran.
- Složitost BFS algoritmu tedy bude \(Θ(L · m + n)\).

Dijkstrův algoritmus

Dijkstra je zobecněním průchodu grafu do šířky.

Místo simulace průchodu BFS vlny v lineárním čase vzhledem k délce hran, Dijkstra zpracuje každou hranu v \(O(1)\) čase.

Vstup: Orientovaný graf \(G = (V, E)\) s kladnými délkami hran \(\ell : E \to \mathbb{R}^+\) a počáteční vrchol \(v_0\).

Výstup:Vzdálenosti z vrcholu \(v_0\) do všech vrcholů grafu \(G\).

Základní idea Dijkstra

U každého původního vrcholu si udržujeme "budík" - kdy by do vrcholu dorazila BFS vlna.
Pokaždé vybereme sousední vrchol s nejmenší hodnotou budíku a podíváme se na jeho následníky.
Pokud by se některý z nich dostal do vrcholu dříve, aktualizujeme jeho budík.
Toto opakujeme dokud "nezazvoní budík" všech vrcholů.

Čas na budíku vrcholu \(v\) ozn. \(h(v)\).
Počáteční hodnota \(h(v_0) = 0\). a \(h(v) = ∞\) pro všechny ostatní vrcholy.
Podobně jako u BFS může mít vrchol tři stavy:
- Nenalezené
- Otevřené (budík je nastavený)
- Uzavřené (budík již zazvonil)
Dále si pamatujeme, který vrchol je předchůdce daného vrcholu na nejkratší cestě.

Dijkstrův algoritmus (pseudokód)

Algoritmus Dijkstra(G, ℓ : E → R+, v0)
 Pro všechny vrcholy v:
     stav(v) := nenalezený
     h(v) := +∞; P (v) := ⊥
 stav(v0) := otevřený
 h(v0) := 0
 Dokud existují nějaké otevřené vrcholy:
     Vyber otevřený vrchol v, jehož h(v) je nejmenší.
     Pro všechny následníky w vrcholu v: //relaxace v
         Pokud h(w) > h(v) + ℓ((v, w)):
             h(w) := h(v) + ℓ((v, w))
             stav(w) := otevřený
             P (w) := v
     stav(v) := uzavřený
 Vrať pole vzdáleností h a pole předchůdců P

Relaxace vrcholů

Přepočítání ohodnocení \(h(w)\) pro všechny následníky \(w\) vrcholu \(v\) v Dijkstra na řádcích (9) – (14) budeme nazývat relaxace vrcholu \(v\)

    Pro všechny následníky w vrcholu v: //relaxace v
        Pokud h(w) > h(v) + ℓ((v, w)):
            h(w) := h(v) + ℓ((v, w))
            stav(w) := otevřený
            P (w) := v
    stav(v) := uzavřený

Konečnost a správnost Dijkstra

Věta o konečnosti Dijkstrova algoritmu

Dijkstra na grafu s kladnými délkami hran se v konečném čase zastaví a po jeho skončení budou všechny dosažitelné vrcholy \(v\) uzavřeny s \(h(v) = d(v_0, v)\).

Tuto větu dokážeme kombinací 4 vlastností Dijkstra:

Vlastnost O (Ohodnocení)
Vlastnost M (Monotonie)
Vlastnost D (Dosažitelnost)
Vlastnost V (Vzdálenost)

Vlastnost O (Ohodnocení)

Ohodnocení \(h(v)\) v průběhu Dijkstra nikdy neroste a je-li konečné, rovná se délce nějakého sledu z \(v_0\) do \(v\).

Důkaz vlastnosti O

Indukcí podle doby běhu Dijkstra.
Na počátku výpočtu tvrzení určitě platí, protože jediné konečné ohodnocení je \(h(v_0) = 0\).
Kdykoliv Dijkstra snižuje ohodnocení \(h(w)\), stane se tak relaxací otevřeného vrcholu \(v\) s konečným \(h(v)\), jehož následníkem je \(w\).
Podle indukčního předpokladu tedy existuje \(v_0-v\)-sled délky \(h(v)\).
Jeho rozšířením o hranu \(vw\) vznikne \(v_0w\)-sled délky \(h(v) + ℓ((v, w))\), což je přesně nová konečná hodnota \(h(w)\).

Vlastnost M (Monotonie)

V každém kroku výpočtu platí, že \(h(z) ≤ h(o)\) pro \(z\) uzavřený vrchol a \(o\) otevřený vrchol. Speciálně pak platí, že Dijkstra nikdy neotevře již uzavřený vrchol.

Důkaz vlastnosti M

Vždy vybereme otevřený vrchol \(v\) s nejmenším \(h(v)\).
Před relaxací \(v\) tedy musí platit \(h(z) ≤ h(v) ≤ h(o)\) pro libovolný \(z\) uzavřený a \(o\) otevřený.
Nyní vrchol \(v\) relaxujeme:
- Pokud \(w\) byl uzavřený, nemůže se jeho hodnota změnit, neboť již před relaxací platilo \(h(w) ≤ h(v)\).
- Pokud \(w\) byl otevřený nebo nenalezený, jeho hodnota se sice může snížit na \(h(v) + ℓ(v, w)\), ale nikdy ne pod \(h(v)\), takže ani pod \(h(z)\) žádného uzavřeného \(z\).
Kdybychom otevřeli již uzavřený vrchol \(z\), muselo by platit \(h(v) + ℓ(v, z) ≤ h(z)\), což nelze.

Vlastnost D (Dosažitelnost)

Když se Dijkstra zastaví, uzavřené jsou právě vrcholy dosažitelné z \(v_0\).

Důkaz vlastnosti D

Dokážeme stejně jako obdobnou vlastnost BFS.
První otevřeným a následně uzavřeným vrcholem je \(v_0\).
Vrchol je otevřen, právě když je do té doby nenalezeným následníkem dříve otevřeného vrcholu a tudíž je dosažitelný z \(v_0\).
Protože Dijkstra dle Vlastnosti M, nikdy neotevře již uzavřený vrchol, zbytek důkazu je totožný s BFS:
- Kdyby tedy existoval nějaký dosažitelný, ale neuzavřený vrchol, existoval by ten „nejbližší“ (co do počtu hran na nejkratší cestě) a to by vedlo ke sporu.

Vlastnost V (Vzdálenost)

Když se Dijkstra zastaví, je \(h(w) = d(v_0, w)\) pro všechny \(w ∈ V\).

Důkaz vlastnosti V

Vrchol \(w\) dosažitelný z \(v_0\) nazveme špatný, pokud \(h(w) \ne d(v0, w)\). Z Vlastnosti O víme, že \(h(w)\) odpovídá délce nějakého \(v_0w\)-sledu a tedy \(h(w) > d(v_0, w)\).

Pro spor předpokládejme, že existuje nějaký špatný vrchol \(w\) (Podobně jako u BFS).
Víme, že v0 není špatný, protože \(h(v_0) = 0 = d(v_0, v_0)\).
Buď \(w\) špatný vrchol takový, že nejkratší cesta v \(G\) z \(v_0\) do \(w\) používá nejmenší možný počet hran.
Buď \(v\) předchůdce \(w\) na této cestě z \(v_0\).
Kdyby \(v\) byl špatný, volili bychom \(v\) namísto \(w\). Tedy platí \(h(v) = d(v_0, v)\).
Vrchol \(v\) byl jistě někdy otevřený a později relaxovaný. Při jeho relaxaci byla aktuální hodnota \(h(w)\) větší než \(d(v_0, w)\) (neboť toto platí dokonce až po zastavení Dijkstra).
V tom případě ale po relaxaci \(v\) muselo platit \(h(w) = d(v_0, v) + ℓ((v, w)) = d(v_0, w)\). Spor.

Vlastnost sledů v Dijkstra

Lemma

Je-li po uzavření vrcholu v algoritmu Dijkstra \(h(v)\) konečné pro nějaký vrchol \(v\), rovná se délce nejkratší \(v_0v\)-cesty, která jako vnitřní vrcholy používá pouze uzavřené vrcholy.

Důkaz vlastnosti sledů v Dijkstra

Indukcí podle počtu uzavřených vrcholů.
Pro \(k = 0\) platí, neboť jediné konečné je \(h(v_0) = 0\).
Pro indukční krok, kdy relaxujeme a tedy uzavíráme \(v\), uvážíme dva případy:
- Relaxace \(v\) nezměnila \(h(w)\). Pak z IP tvrzení platí.
- Relaxace \(v\) změnila \(h(w)\). Pak dle Vlastnosti O \(h(w)\) odpovídá délce nejkratší \(v_0v\)-cesty protažené o hranu \((v, w)\).
- Protože nyní ale je \(v\) uzavřený a \(v_0v\)-cesta (dle IP) používala jako vnitřní vrcholy jen uzavřené vrcholy, platí tato vlastnost i pro \(w\).

Složitost Dijkstra bez binární haldy (priority queue)

Pokud jsou délky hran kladné, potom Dijkstra nad souvislým grafem o \(n\) vrcholech běží v čase \(O(n^2)\).

V grafech s malým počtem hran je odhad \(O(n^2)\) zbytečně nadhodnocený. Celkový počet operací na řádku (11) je pouze \(O(m)\), ale brzdí nás hledání minima: \(O(n)\).

Důkaz složitosti Dijkstrova algoritmu

Inicializace trvá \(O(n)\).
Každý vrchol uzavřeme nejvýše jednou.
Vnějším cyklem projdeme nejvýše \(n\)-krát.
Pokaždé hledáme minimum až z \(n\) ohodnocení vrcholů a procházíme až \(n\) následníků.

Dijkstra s binární haldou

Podobně jako u Jarníkova algoritmu, použijeme (binární) haldu, klíčem \(v\) bude hodnocení \(h(v)\).

Dijkstra s binární haldou

Algoritmus DijkstraHalda(G, ℓ : E → R+, v0)
Pro všechny v ∈ V:
    h(v) := +∞; P(v) := ⊥
h(v0) := 0
H := HeapBuild(V) uspořádanou podle klíčů h
Dokud H neprázdná:
    v := HeapExtractMin(H)
    Pro všechny následníky w vrcholu v:
        Pokud w ∈ H & h(w) > h(v) + ℓ((v, w)):
            P(w) := v
            HeapDecreaseKey(H, w, h(v) + ℓ((v, w)))
Vrať P a h

Věta o časové složitosti Dijkstra s binární haldou

Časová složitost DijkstraHalda je \(O(|E| \log |V|)\).

Důkaz

Řádky (2)-(5) trvají \(O(|V|)\).
Celková složitost na řádku (7) je \(O(|V| \log |V|)\).
Celková složitost na řádku (11) je \(O(|E| \log |V|)\), neboť počet volání operace HeapDecreaseKey je nejvýše \(|E|\).