12.1 Ohodnocený graf

Definice 12.1 (Ohodnocený orientovaný graf)

Ohodnocený orientovaný graf

• Mějme orientovaný graf \(G = (V, E)\). Každé hraně \(e \in E\) přiřadíme číselnou váhu \(w(e)\), kde \(w: E \to R\). Takový graf se nazývá hranově ohodnocený.
• Váhovou funkci můžeme přirozeně rozšířit na podgrafy: Váha \(w(H)\) podgrafu \(H \subseteq G\) je součet vah jeho hran.
• Vstup pro problém nejkratších cest je podobný. Ohodnocení hrany interpretujeme jako její délku, značíme ℓ(e).
• Délku hrany můžeme přirozeně rozšířit i na cesty: délka cesty je součet délek jejích hran.

  V přednášce definováno pomocí definice z problému minimální kostry.

Definice 12.2 (Vzdálenost v ohodnoceném grafu)

Vzdálenost v ohodnoceném grafu

Pro libovolné dva vrcholy u a v ohodnoceného orientovaného grafu, vzdálenost \(d(u, v)\) je minimum z délek všech \(uv\)-cest (cest z \(u\) do \(v\)), případně +∞, pokud žádná \(uv\)-cesta neexistuje.

Definice 12.3 (Nejkratší cesta v ohodnoceném grafu)

Nejkratší cesta v ohodnoceném grafu

je libovolná \(uv\)-cesta, jejíž délka je rovná vzdálenosti \(d(u, v)\).

Definice 12.4 (Sled v ohodnoceném grafu)

Sled v ohodnoceném grafu

Posloupnost (\(v_0\), \(e_1\), \(v_1\), . . . , \(e_k\), \(v_k\)) v orientovaném grafu \(G = (V, E)\) se nazývá \(v_0v_k\)-sled (nebo krátce sled), pokud \(vi ∈ V\) pro všechna \(i ∈ {0, . . . , k}\) a \(e_i = (v_{i−1}, v_i) ∈ E\) pro všechna \(i ∈ {1, . . . , k}\).

Délka \(ℓ(S)\) sledu \(S\) je součet délek jeho hran.

Lemma (o zjednodušení sledů)

Lemma (o zjednodušení sledů)

Pokud jsou délky hran kladné, pak pro každý \(uv\)-sled existuje \(uv\)-cesta stejné nebo menší délky.

Důkaz věty 12.1

• Pokud sled není cestou, znamená to, že se v něm opakují vrcholy.
• Označme tedy t první vrchol (v pořadí od u), který se opakuje.
• Část sledu mezi prvním a posledním výskytem vrcholu \(t\) vystřihneme a získáme \(uv\)-sled stejné nebo menší délky, protože délky hran jsou kladné.
• Přitom ubyla alespoň jedna hrana, takže opakováním tohoto postupu časem dostaneme cestu.

Důsledek - Nejkratší cesta

Pokud jsou délky hran v \(G = (V, E)\) kladné, pak pro libovolné dva vrcholy \(u, v ∈ V\) existuje nejkratší \(uv\)-sled a ten je současně nejkratší \(uv\)-cestou.

Důkaz

• Nejkratší cesta je jedním ze sledů.
• Pokud by tvrzení neplatilo, musel by existovat nějaký kratší sled. Ten by ovšem, podle předchozího lemmatu, šel zjednodušit na ještě kratší cestu.

Důsledek - Trojúhelníková nerovnost

Jsou-li délky hran kladné, platí pro vzdálenosti trojúhelníková nerovnost: \(d(u, v) ≤ d(u, w) + d(w, v)\) pro libovolné \(u, v, w ∈ V\) .

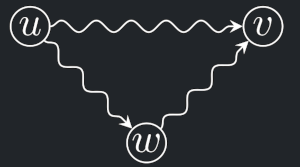
Důkaz

• Pokud je \(d(u, w)\) nebo \(d(w, v)\) nekonečná, nerovnost triviálně platí.
• V opačném případě uvažme spojení nejkratší \(uw\)-cesty s nejkratší \(wv\)-cestou. To je nějaký \(uv\)-sled délky \(d(u, w) + d(w, v)\) a ten, podle předchozího důsledku, nemůže být kratší než nejkratší \(uv\)-cesta, která má délku \(d(u, v)\).

Důsledek - Vrcholy na nejkratší cestě

Nechť jsou délky hran kladné, \(P\) je nejkratší \(uv\)-cesta a \(w\) leží na \(P\). Označme \(P_{uw}\) část \(P\) mezi \(u\) a \(w\) a \(P_{wv}\) část \(P\) mezi \(w\) a \(v\). Pak \(P_{uw}\) je nejkratší \(uw\)-cesta a \(P_{wv}\) je nejkratší \(wv\)-cesta.