11.6 Union Find pokračování

Implementace struktury Union-Find pomocí pole

• Triviální přístup: použijeme pole, které každému elementu přiřadí číslo jeho množiny.
• Find přečte číslo množiny z pole v konstantním čase.
• Union při slučování množin projde všechny elementy jedné množiny a přiřadí jim číslo té druhé.

Pozorování

Při reprezentaci polem je časová složitost

• Init\(T_i(n) = O(n)\),
• Find\(T_f(n) = O(1)\) a
• Union\(T_u(n) = O(n)\).

Časová složitost Kruskalova algoritmu by tedy byla \(O(m \log n + n + m + n^2) = O(m \log n + n^2)\).

---

Implementace struktury Union-Find pomocí keříků

• Každou množinu, budeme reprezentovat stromem orientovaným směrem do kořene – budeme jim říkat keříky.
• Založená struktura je les, který má jednovrcholový strom za každý element universa.
• Vrcholy keříku odpovídají elementům příslušné množiny.
• Jako identifikátory množin použijeme element uložený v kořeni daného keříku.
• V paměti budeme keříky reprezentovat úsporně: každý element v si pamatuje „pouze“ identifikátor svého otce \(p(v)\).
• Kořeny keříků \(v\) mají \(p(v) = \bot\).

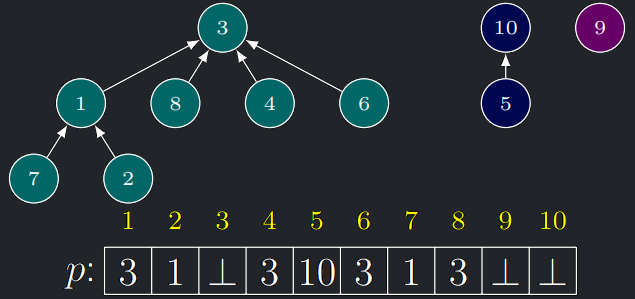
Find s keříky

• Operace Find(u) postupně vystoupá ze zadaného elementu u do kořene keříku a vrátí tento kořen.

Algoritmus 11.4 (Union-Find: Find s keříky)

Dokud p(u) ̸= ⊥:
    u := p(u)
 Vrať u

Pozorování

Časová složitost Find(\(u\)) je \(O(\)hloubka keříku elementu \(u)\).

Union s keříky

• Do kořene \(v\) každého keříku uložíme hloubku keříku \(H(v)\).
• Na počátku mají všechny keříky hloubku \(1\).
• Při slučování různě hlubokých keříků připojíme mělčí keřík pod kořen toho hlubšího a hloubka toho hlubšího se nezmění.
• Jsou-li oba keříky stejně hluboké, rozhodneme se libovolně a výsledný keřík má hloubku o jedna větší.

Algoritmus 11.4 (Union-Find: Union s keříky)

a := Find(u)
b := Find(v)
Je-li a = b, skonči
Pokud H(a) = H(b):
    H(a) := H(a) + 1
    p(b) := a
    skonči
Pokud H(a) < H(b):
    p(a) := b
Pokud H(a) > H(b):
    p(b) := a

Hloubka keříků

Lemma 11.8 (o hloubce keříků)

Výše popsaný algoritmus Union zachovává invariant, že keřík s \(h\) hladinami obsahuje nejméně \(2^{h−1}\) vrcholů.

Důkaz lemmatu 11.8

• Indukcí podle počtu operací Union.
• Na počátku algoritmu mají všechny keříky jednu hladinu a \(1\) vrchol a \(( 1 \ge 2^{1−1} = 1)\).
• Nechť nyní provádíme Union\((u,v)\) a počet hladin obou keříků je různý.
• Připojením mělčího keříku pod kořen toho hlubšího se počet hladin nezmění a počet vrcholů neklesne, takže nerovnost stále platí.
• Pokud mají oba keříky \(h\) hladin, platí z indukčního předpokladu, že každý z nich obsahuje minimálně \(2^{h−1}\) vrcholů.
• Jejich sloučením tudíž vznikne keřík s \(h + 1\) hladinami o alespoň \(2 \cdot 2^{h−1} = 2^h\) vrcholech.

Důsledek

Hloubka keříků během provádění výše popsaného algoritmu Union\((u,v)\) nepřekročí \(\log n\).

Důkaz důsledku

Strom s větším počtem hladin by podle invariantu obsahoval více než n vrcholů

Složitost Kruskalova algoritmu s keříky

• Z předchozího plyne, že v keříkové reprezentaci je časová složitost operace

  • Init \(T_i(n) = O(n)\),
  • Find \(T_f(n) = O(\log n)\) a
  • Union \(T_u(n) = O(\log n)\) (my dokonce voláme jen na kořeny, takže lze počítat \(O(1)\)).

• A proto dostaneme

\[O(m \log n + T_i(n) + m \cdot T_f(n) + n \cdot T_u(n)) =\]

\[O(m \log(n) + n + m \cdot log(n) + n \cdot log(n)) \in O(m \log n)\]

Důsledek (věty o časové složitosti Kruskalova algoritmu)

Kruskalův algoritmus s keříkovou strukturou pro Union-Find vytvoří minimální kostru v čase \(O(|E| \log|V|)\).

---

Struktura Union-Find obecně

• Kruskalův algoritmus je velmi známá aplikace datové struktury Union-Find, ale ne jediná.
• Struktura Union-Find je vhodná a přirozená pro algoritmické (snadno paralelizovatelné) řešení dalších problémů, např.
  • Konstrukce souvislých komponent grafu.
  • Detekce cyklu v grafu.
  • Konstrukce bludiště.
  • Odvozování typu proměnných v dynamických programovacích jazycích.