11.4 Kruskalův algoritmus

Algoritmus 11.2 (Kruskalův)

Algoritmus Kruskal

Vstup

Souvislý hranově ohodnocený graf \(G = (V,E)\). Nechť \(n = |V|\) a \(m = |E|\).

Výstup

Minimální kostra \(G\)

Idea

• Kruskalův algoritmus je také založen na hladovém přístupu:začne lesem tvořeným pouze samotnými vrcholy bez hran a zkouší přidávat hrany od nejlehčí po nejtěžší a zahazuje ty, které by vytvořily cyklus.

Algoritmus

Seřaď hrany podle vah: w(e1) ≤ · · · ≤ w(em)
T := (V, ∅) //počáteční les bez hran
Pro i := 1, . . . , m opakuj:
    označ u, v krajní vrcholy hrany ei
    Pokud u a v leží v různých komponentách lesa T:
        E(T) := E(T) ∪ {ei}
Vrať T

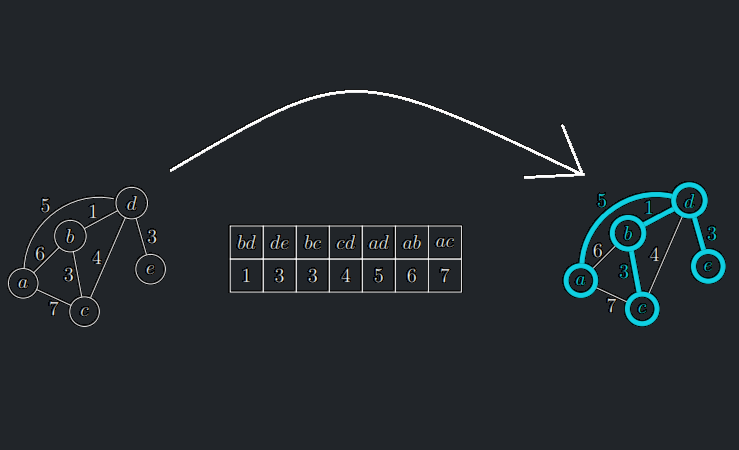
Lemma 11.6 (o korektnosti Kruskalova algoritmu)

Kruskalův algoritmus se zastaví a vydá minimální kostru.

Důkaz lemmatu 11.6

• Konečnost: cyklus se vykoná \(m\)-krát.
• Správnost: Ukážeme nejdříve, že pokud algoritmus přidá hranu \(e = \{u,v\}\) do \(T\), pak \(e\) leží v minimální kostře.
• Pokud algoritmus \(e\) přidá, stane se tak v okamžiku, kdy se vrcholy \(u\) a \(v\) nacházejí v nějakých dvou rozdílných stromech \(T_u\) a \(T_v\) lesa \(T\).
• Hrana \(e\) přitom leží v elementárním řezu oddělujícím strom \(T_u\) od zbytku grafu.
• Hrana \(e\) musí být nejlehčí hrana elementárního řezu oddělujícího strom \(T_u\) od zbytku grafu, neboť případnou lehčí hranu by algoritmus potkal dříve a přidal by ji do \(T\).
• Hrana \(e\) tedy leží v minimální kostře podle lemmatu o řezech.
• Nyní si ukážeme, že výsledný \(T\) je souvislý.
• Pokud by nebyl, uvažme dva rozdílné stromy \(T_u\) a \(T_v\) lesa \(T\) a elementární řez oddělující strom \(T_u\) od zbytku grafu.
• Protože je graf \(G\) souvislý, je tento elementární řez neprázdný a má nějakou hranu \(e\).
• Když algoritmus zkoumal hranu \(e\), nemohla tvořit cyklus (netvoří ho ani ve výsledném \(T\)), takže by ji algoritmus musel přidat, což je spor.
• Výstupem algoritmu je tedy kostra, která je podgrafem minimální kostry – tedy minimální kostra.