11.2 Jarníkův algoritmus

Nejjednodušší algoritmus pro hledání minimální kostry pochází z roku 1930, kdy ho vymyslel český matematik Vojtěch Jarník.
Tehdy myšlenka zapadla a až později byla několikrát znovuobjevena – proto se algoritmu říká též Primův.

Algoritmus 11.1 (Jarníkův)

Algoritmus Jarník

Vstup

Souvislý hranově ohodnocený graf \(G\)

Výstup

Minimální kostra \(G\)

Idea

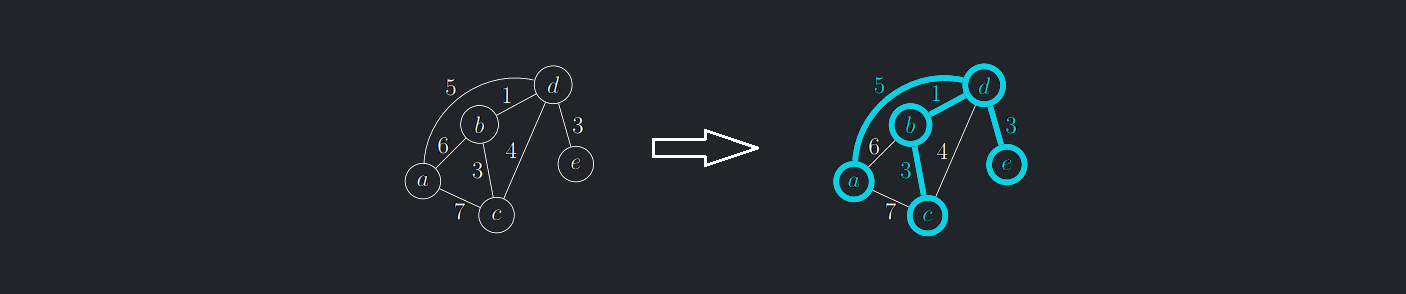
Začneme se stromem, který obsahuje libovolný jeden vrchol a žádné hrany.
Vybereme nejlehčí hranu incidentní s tímto vrcholem.
Přidáme ji do stromu i s novým koncovým vrcholem.
Postup opakujeme: v každém dalším kroku přidáváme nejlehčí z hran, které vedou mezi vrcholy dosud vytvořeného stromu a zbytkem grafu.
Takto pokračujeme, dokud nevznikne celá kostra.

Algoritmus

Algoritmus MinKostraJarník (G = (V, E), w: E → R):

v0 := libovolný vrchol grafu
T := strom obsahující pouze vrchol v0 a žádné hrany
Dokud existuje hrana {u, v} taková, že u ∈ V(T) a v ̸∈ V(T)
    Přidej nejlehčí takovou hranu spolu s v do T
Vrať T

Image title

Hladové algoritmy

Jarníkův algoritmus je typickým příkladem tzv. hladového algoritmu (angl. greedy algorithm).
V každém okamžiku vybíráme lokálně nejlepší hranu.
Minimální kostra je jedním z řídkých případů, kdy hladový algoritmus skutečně spočte optimální řešení.
Dokážeme postupně, že Jarníkův algoritmus skutečně vrátí minimální kostru.

Důkaz korektnosti Jarníkova algoritmu

Nejprve ukážeme, že se Jarníkův algoritmus spuštěný na souvislém hranově ohodnoceném grafu zastaví a vygeneruje kostru.
Dále budeme pro jednoduchost předpokládat hranově ohodnocený graf s unikátními vahami a dokážeme, že má jedinou minimální kostru a Jarníkův algoritmus ji vytvoří.
K tomu zavedeme pojem elementárního řezu grafu.
Poté ukážeme, že Jarníkův algoritmus vydá minimální kostru i v případě, že váhy nejsou unikátní (viz graf v předchozím příkladu).

1. Konečnost Jarníkova algoritmu

Lemma 11.1 (o konečnosti Jarníkova algoritmu)

Lemma o konečnosti Jarníkova algoritmu

Jarníkův algoritmus se po \(|V| - 1\) iteracích zastaví a vydá nějakou kostru zadaného grafu \(G = (V, E)\).

Důkaz Lemmatu 11.1

Graf \(T\) konstruovaný algoritmem vzniká z jednoho vrcholu postupným přidáváním listů.
Takže \(T\) je v každém okamžiku výpočtu strom.
V každé iteraci se \(|V(T)|\) zvětší o \(1\).
Dokud \(V(T) \ne V(G)\), musí díky souvislosti \(G\) existovat hrana mezi \(V(T)\) a \(V(G) \setminus V(T)\), kterou může algoritmus přidat do \(T\).
To znamená, že algoritmus se zastaví, až když \(V(T) = V(G)\).
Tehdy je ale \(T\) kostra.

2. Správnost Jarníkova algoritmu

Definice 11.2 (Elementární řezy v grafu)

Elementární řezy v grafu

Nechť A je nějaká podmnožina vrcholů grafu \(G = (V, E)\) a \(B\) její doplněk, tj. \(B = V \setminus A\). Množině všech hran, které leží jedním vrcholem v \(A\) a druhým v \(B\), budeme říkat elementární řez grafu \(G\) určený množinami \(A\) a \(B\).

Lemma 11.2 (o řezech v grafu s unikátními vahami)

Lemma o řezech v grafu s unikátními vahami

Nechť \(G\) je souvislý ohodnocený graf s unikátními vahami, \(R\) nějaký jeho elementární řez a \(e\) nejlehčí hrana tohoto řezu. Pak (každá) minimální kostra grafu \(G\) obsahuje hranu \(e\).

Důkaz Lemmatu 11.2

Dokážeme obměněnou implikaci: Pokud nějaká kostra \(T\) neobsahuje hranu \(e\), pak není minimální.
Označme \(A\) a \(B\) množiny vrcholů určující elementární řez \(R\).
Hrana \(e = \{a,b\}\), \(a \in A\), \(b \in B\), je nejlehčí v \(R\).
Nechť \(T\) je kostra neobsahující \(e\).
Protože \(T\) je strom, existuje v něm jediná cesta \(P(a,b)\) a ta musí alespoň jednou překročit elementární řez \(R\).
Nechť \(f = \{a^′,b^′\}\), \(a^′ \in A\), \(b^′ \in B\), je libovolná hrana, kde se to stalo.

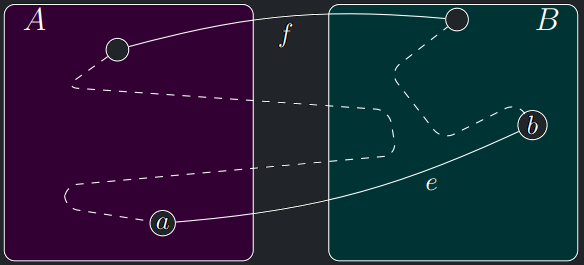
Element rezy

Nyní z kostry \(T\) odebereme hranu \(f\).
Tím se kostra rozpadne na dva stromy \(T_a\), \(T_b\), z nichž jeden obsahuje \(a\) a druhý \(b\).
Přidáním hrany \(e\) stromy opět propojíme a tím získáme jinou kostru \(T^′\).
Platí \(w(T^′) = w(T) − w(f) + w(e)\).
Protože e je nejlehčí hrana v elementárním řezu a váhy jsou unikátní, musí platit \(w(f) \gt w(e)\).
Proto \(w(T^′) \lt w(T)\) a tudíž \(T\) není minimální kostra.

Varování

Zmínka existence jediné cesty \(P(a,b)\) a následné vybrání hrany \(f\), která leží někde na této cestě je důležitá.

Pouhé vybrání náhodné hrany \(f\) (která překračuje elementární řez) a následné prohození \(f\) a \(e\) by nevedlo ke správnému závěru.

Věta 11.3 (o minimální kostře Jarník)

Věta o minimální kostře Jarník

Souvislý graf s unikátními vahami má právě jednu minimální kostru a Jarníkův algoritmus tuto kostru vytvoří.

Důkaz Věty 11.3

Jarníkův algoritmus v každém kroku vybere jedinečnou nejlehčí hranu elementárního řezu mezi vrcholy dosud vytvořeného stromu a zbytkem grafu, která je vždy dle lemmatu obsažena v každé minimální kostře.
To ale znamená, že kostra vytvořená Jarníkovým algoritmem je podgrafem každé minimální kostry.
Protože ale všechny kostry daného grafu mají stejný počet hran, znamená to, že vytvořená kostra je všem minimálním kostrám rovna a je tudíž unikátní.

Důsledek

Minimální kostra je jednoznačně určena uspořádáním hran podle vah, na konkrétních hodnotách vah nezáleží. Toto platí neboť Jarníkův algoritmus váhy hran mezi sebou pouze porovnává.

Pokud tedy pro každý elementární řez grafu G existuje právě jedna nejlehčí hrana, pak má G právě jednu minimální kostru.
Protipříklad na obrázku výše ale ukazuje, že neplatí obrácená implikace, tedy: Pokud má graf G právě jednu minimální kostru, pak pro každý elementární řez grafu G (ne)existuje právě jedna nejlehčí hrana.

Korektnost Jarníkova algoritmu pro neunikátní váhy

Pokud nejsou váhy unikátní, může v dané iteraci existovat několik nejlehčích hran \(\{a, b\}\), \(a \in V(T)\), \(b \notin V(T)\) a Jarníkův algoritmus vždy jednu z nich vybere.
Lemma o řezech stačí upravit následovně.

Lemma 11.4 (o řezech v grafu s opakujícími se vahami hran)

Lemma o řezech v grafu s opakujícími se vahami hran

Nechť \(G\) je souvislý ohodnocený graf, \(R\) je elementární řez v \(G\) a \(e\) je libovolná nejlehčí hrana v \(R\). Pro každou minimální kostru \(T^′\) existuje minimální kostra \(T\) taková, že

\(T^′\) a \(T\) se mohou lišit pouze na hranách obsažených v \(R\) a
\(T\) obsahuje \(e\)

Důkaz Lemmatu 11.4

Označme \(A\) a \(B\) množiny vrcholů, kterými je určen elementární řez \(R\).
Nechť \(T^′\) neobsahuje \(e\) a nechť \(e = \{a,b\}\).
Buď \(P\) unikátní cesta mezi vrcholy \(a\) a \(b\) v \(T^′\).
Cesta \(P\) prochází elementárním řezem \(R\).
Nechť \(f\) je libovolná hrana v \(E(P) \cap R\).
Potom \(T := T^′ − f + e\) je kostra a platí, že \(w(T) \le w(T^′)\).

Důsledek

Pokud G obsahuje více minimálních koster díky existenci hran se stejnou vahou, pak Jarníkův algoritmus jednu z nich zkonstruuje.

Složitost Jarníkova algoritmu

Pozorování

Naivní implementace Jarníkova algoritmu nad grafem \(G = (V,E)\), reprezentovaným seznamem sousedů má časovou složitost \(O(|V| \cdot |E|)\) (\(|V|\) krát hledáme nejlehčí hranu v seznamu nejvýše \(|E|\) hran) a paměťovou složitost \(O(|V| + |E|)\).