11.1 Problém minimální kostry grafu
Motivace
- Napadl sníh a všechny ulice města jsou zasněžené.
- Které ulice prohrneme, aby šlo dojet odkudkoliv kamkoliv, a přitom nám prohrnutí sněhu dalo co nejméně práce?
-
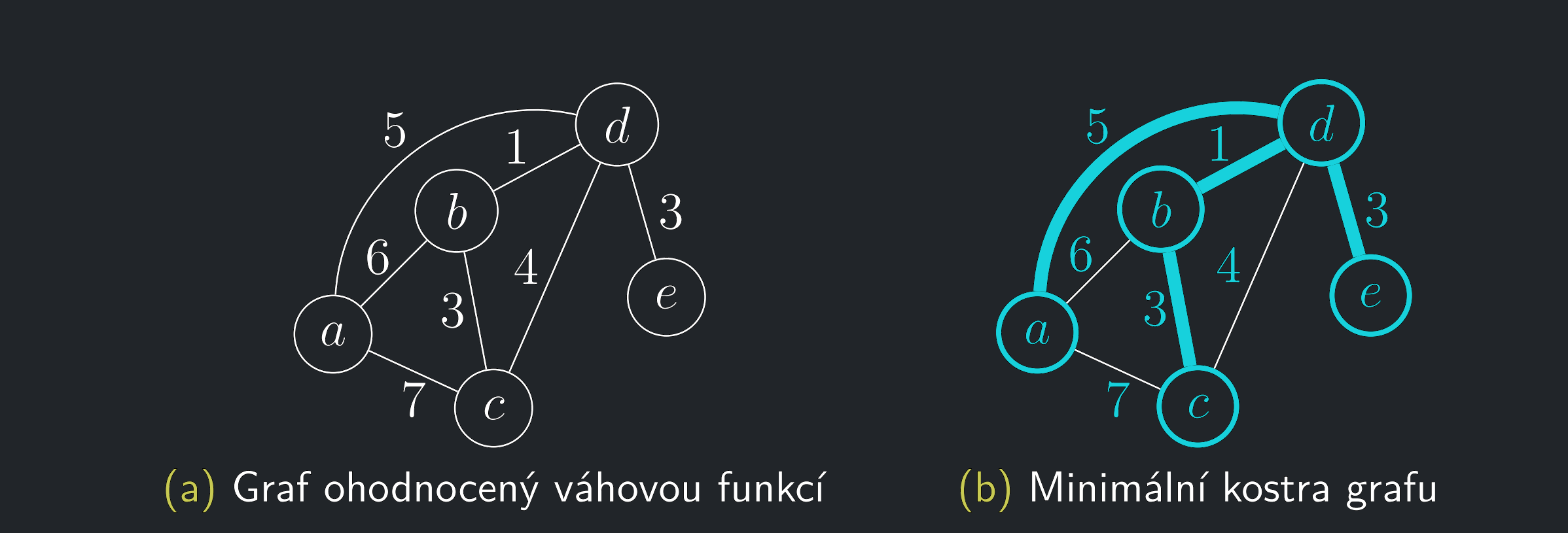
Tato otázka vede na hledání tzv. minimální kostry grafu.
-
Popišme nyní problém formálně.
- Připomenutí: Kostra grafu \(G\) je podgraf, který obsahuje všechny vrcholy a je to strom, a má tedy \(|V (G)| − 1\) hran.
Definice 11.1 (Minimální kostra grafu)
Minimální kostra grafu
- Mějme souvislý neorientovaný graf \(G = (V, E)\). Každé hraně \(e \in E\) přiřadíme číselnou váhu \(w(e)\), kde \(w: E \to \mathbb{R}\). Takový graf se nazývá hranově ohodnocený.
- Váhovou funkci můžeme přirozeně rozšířit na podgrafy: Váha \(w(H)\) podgrafu \(H \subseteq G\) je součet vah jeho hran.
- Kostra hranově ohodnoceného grafu G je minimální, pokud má mezi všemi jeho kostrami nejmenší váhu.