Skip to content

10.6 Triangulace konvexního mnohoúhelníku

Definice 10.1 (Triangulace)

Nechť \(U\) je konvexní \(n\)-úhelník, \(n \gt 3\), zadaný kartézskými souřadnicemi vrcholů \(a_1, a_2,\dots, a_n\) v rovině číslovanými proti směru hodinových ručiček. Pak

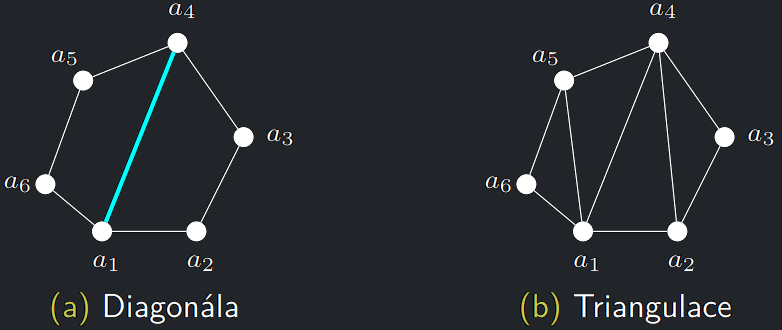
  • Diagonála \(a_ia_j\) = úsečka spojující 2 nesousední vrcholy \(a_i, a_j\).
  • Triangulace \(U\) = taková podmnožina jeho diagonál, která rozděluje plochu \(U\) na trojúhelníky a ve které se žádné dvě diagonály neprotínají (až na své koncové vrcholy).

ukázka triangulace

Pozorování

Každá triangulace \(n\)-úhelníku sestává z \(n − 3\) diagonál a dělí \(U\) na \(n − 2\) trojúhelníků.

Definice 10.2 (Vlastnosti triangulace)

  • Délku diagonály \(a_ia_j\) značíme \(\Vert a_ia_j \Vert\).
  • Velikost triangulace je součet délek jejích diagonál.
  • Minimální triangulace mnohoúhelníku (MTM) \(U\) je ta z triangulací \(U\), která má minimální velikost.

Problém minimální triangulace mnohoúhelníku

  • Na vstupu je konvexní \(n\)-úhelník \(U\) zadaný kartézskými souřadnicemi vrcholů \(a_1, a_2,\dots, a_n\) v rovině.
  • Úkolem je určit velikost jeho minimální triangulace, případně takovou triangulaci vypsat.

Velikost MTM - myšlenka

  • Ke každé hraně mnohoúhelníku v každém řešení „přiléhá“ jeden trojúhelník.
  • Speciálně je to pravda pro hranu \(a_1a_n\) na kterou se zaměříme.
  • Zvolíme-li libovolný takový trojúhelník \(T\), rozdělíme mnohoúhelník \(U\) na dva menší
    (z nichž některý může být prázdný).

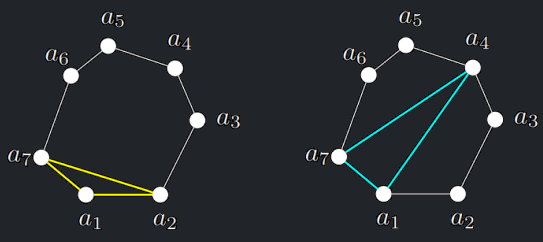
ukázka triangulace

  • Každá triangulace se skládá z diagonál obsažených v nějakém trojúhelníku \(T\) a z triangulace menšího mnohoúhelníka nebo obou menších mnohoúhelníků
  • Minimální triangulace se tedy skládá z diagonál obsažených v nějakém trojúhelníku \(T\) a z minimálních triangulací menších mnohoúhelníků. Tyto triangulace najdeme rekurzivně.
  • Protože dopředu nevíme, který trojúhelník patří do minimální triangulace, musíme vyzkoušet všechny.

Algoritmus 10.12 (MtmRec)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
MtmRec(a_1,..., a_n)
    Pokud n = 3: Vrať 0
    M := ∞
    Pro k := 2,...,n − 1:
    // hrana a_1,a_n bude v trojúhelníku a_1,a_n,a_k,
    // ten rozdělí a_1,...,a_n na a_1,...,a_k a a_k,...,a_n.
        Pokud k = 2: M_1 := 0
        Pokud k ≥ 3: M_1 := MtmRec(a_1,...,a_k) + ||a_1,a_k||
        Pokud k ≤ n − 2: M_2 := MtmRec(a_k,...,a_n) + ||a_k,a_n||
        Pokud k = n − 1: M_2 := 0
    M := min(M, M_1 + M_2)
    Vrať M

Fakt o počtu různých triangulací

Počet různých triangulací konvexního \(n\)-úhelníku je dán \((n − 2)\)-tým
Catalanovým číslem \(C(n - 2) = \frac{1}{n-1} \binom{2n-4}{n-2} = 2^{\Theta(n)}\)

Důsledek faktu o počtu triangulací

MtmRec má exponenciální časovou složitost.

Velikost MTM - memoizace

  • Definujeme nyní hodnoty \(M[i, j]\) jako
    • velikost minimální triangulace mnohoúhelníku \(a_i ,\dots, a_j\).
  • Číslo \(M[i, j]\) má smysl pro \(j \gt i + 2\) (mnohoúhelník je tvořen aspoň třemi vrcholy).
  • Zjevně \(M[i, i + 2] = 0\).
  • Hodnota \(M[1, n]\) představuje velikost minimální triangulace celého \(a_1,\dots, a_n\), tedy řešení úlohy Velikost MTM.
  • Hodnoty \(M[i, j]\) budeme počítat postupně podle velikosti mnohoúhelníka, tedy podle rozdílu \(j − i\).
  • Obecně, při výpočtu \(M[i, j]\) je třeba zkusit všechny trojúhelníky \(T\), které přiléhají stranou k úsečce \(a_ia_j\).
  • Jejich třetí vrchol \(a_k\) je některý z \(a_{i+1}, a_{i+2},\dots, a_{j−1}\), čili \(k \in \{i + 1,\dots, j − 1\}\).

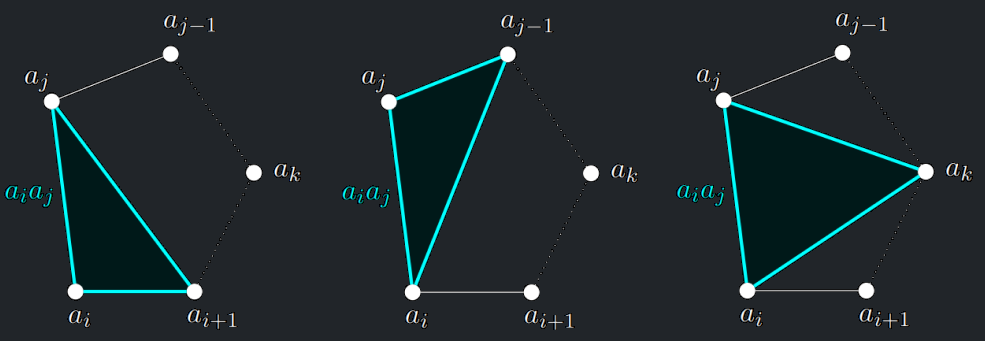
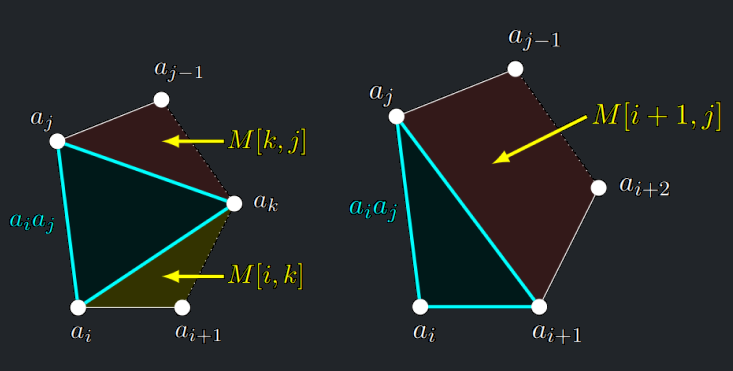
ukázka principu_iterace

  • Pokud třetí vrchol \(a_k\) je některý z \(a_{i+2},\dots, a_{j−2}\), pak trojúhelník \(T\) rozdělí zkoumaný mnohoúhelník na dva menší mnohoúhelníky, jejichž optimální triangulace jsme již spočítali dříve.
  • Takže hledáme \(k\), které vede na minimum výrazu
\[ M[i, j] = \min_{i+2 \le k \le j-2} (M[i, k] + \Vert a_i a_k \Vert + M[k,j] + \Vert a_k a_j \Vert) \]

ukázka principu_iterace

Algoritmus MtmIter

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
MtmIter(a_1,..., a_n)
    Pro i := 1,..., n:
    M[i, i + 2] := 0
    Pro s := 4,..., n:  //velikost mnohoúhelníka
        Pro i := 1,..., n − s + 1:
            j := i + s − 1
            M[i, j] := ∞
            Pro k := i + 1,..., j − 1:
                Pokud k = i + 1: M_1 := 0
                Pokud k ≥ i + 2: M_1 := M[i, k] + ||a_i,a_k||
                Pokud k ≤ j − 2: M_2 := M[k, j] + ||a_k,a_j||
                Pokud k = j − 1: M_2 := 0
                M[i, j] := min(M[i, j], M_1 + M_2)
    Vrať M[1, n]

Pozorování o časové složitosti MtmIter

Časová složitost algoritmu MtmIter je \(O(n^3)\) a paměťová \(O(n^2)\).