10.5 Optimalizace BVS

Pro danou množinu hodnot není BVS jednoznačně určený.
Ne vždy je nejdůležitějším faktorem hloubka celého stromu.
Občas je důležitá hloubka daného prvku/klíče a frekvence jeho vyhledávání.
Mějme data obsahující prvky 8, 11, 16, 20, 25.
Nechť je vypozorováno v posledních tisíci vyhledáváních, že prvek 8 je vyhledáván 100krát, prvek 11 je vyhledáván 250krát a další prvky po řadě 50, 400 a 200krát.

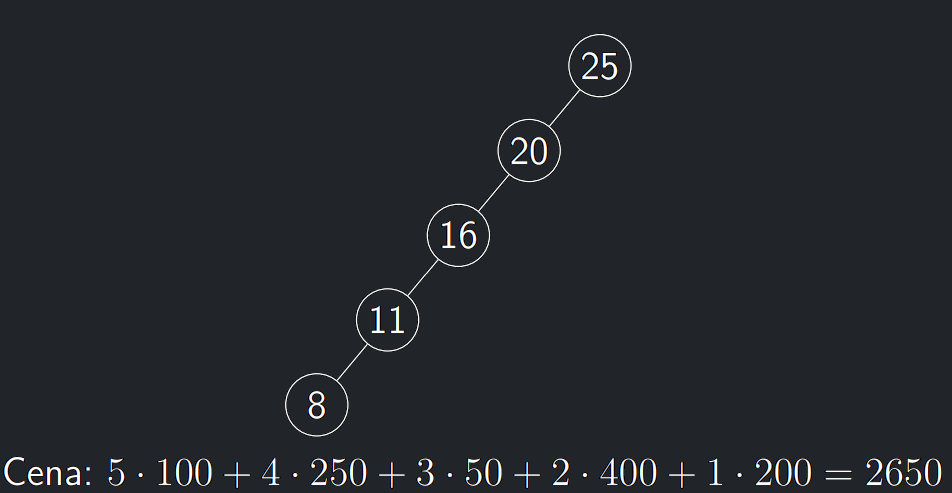
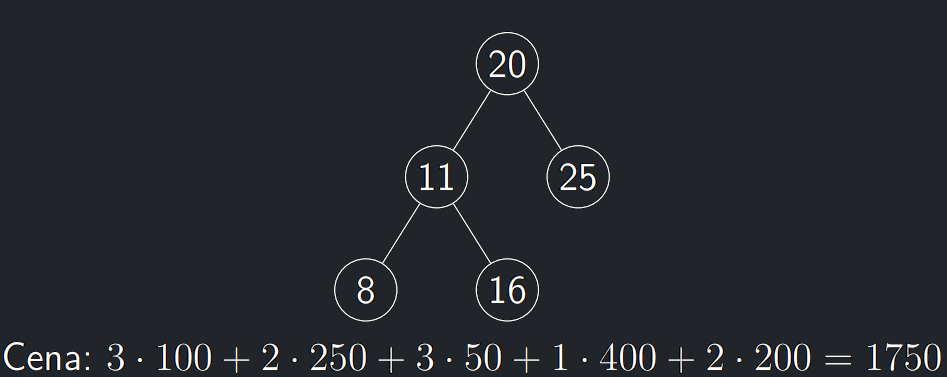
bvs_optimal

Histogramové BVS - myšlenka

Hledané BVS musí mít nějaký kořen.
Jelikož kořen neznáme a protože není vůbec jasné jak poznat správný kořen, rezignujeme a „prostě vyzkoušíme všechny“.
Jestliže jsme jako kořen zvolili hodnotu r, rozdělí se naše data na
dvě části $L = {1, \dots, r - 1}$ a $R = {r + 1, \dots, n}$ .
Naším dalším úkolem pak bude naleznout nejlepší možné stromy $T_{L}$ a $T_{R}$ pro tato data a získat výsledek.
Data obsažená v $L$ i v $R$ získají jedno vyhledávání navíc.

1 \cdot p_{r} + \sum_{i \in L} (1 + h_{L} (i)) p_{i} + \sum_{i \in R} (1 + h_{R} (i)) p_{i} = \sum_{i \in [n]} p_{i} + \sum_{i \in L} h_{L} (i) p_{i} + \sum_{i \in R} h_{R} (i) p_{i}

kde $h_{L} (i)$ a $h_{R} (i)$ označují příslušné hladiny ve stromech pro data v $L$ a $R$ .

Algoritmus 10.10 (BVSOPT_rec)

BVSOPT_rec(p_1,...,p_n)
    Pokud n = 0: Vrať 0
    x := Sum(i∈[n], p_i)
    m := +∞
    Pro r = 1,...,n:
        L := {p_1,..., p_{r−1}}, R := {p_{r+1},..., p_n}
        c_L := BVSOPT_rec(L)
        c_R := BVSOPT_rec(R)
        m := min(m, c_L + c_R)
    Vrať m + x

Pozorování o BVSOPT_rec

BVSOPT_rec(p_1,...,p_n) je konečný a vrací hodnotu nějakého BVS.

Lemma o korektnosi BVSOPT_rec

BVSOPT_rec(p_1,...,p_n) vrací hodnotu optimálního řešení.

Důkaz korektnosti BVSOPT_rec

BVSOPT_rec(p_1,...,p_n) vrací hodnotu pro nějaký BVS a tedy speciálně vrací horní odhad na optimum.
Obráceně pak uvažme nějaké optimální řešení – tedy binární vyhledávací strom $T$ .
Formálně dokazujeme indukcí podle velikosti (tj. počtu vrcholů) stromu $T$ .

ZI: Pro jednovrcholové stromy jistě vrací optimální řešení.

IK:

Nechť tedy $T$ má alespoň 2 vrcholy a nechť $r$ je jeho kořen (BVSOPT_rec zkouší $r$ ).
Dále se strom $T$ skládá z levého podstromu $T_{L}$ , který obsahuje data $L$ (obdobně pro $R$ ).
Protože $T_{L}$ má alespoň o jeden vrchol méně než $T$ , lze na něho aplikovat indukční předpoklad, tedy BVSOPT_rec(L) vrátí hodnotu optimálního řešení (nanejvýš takové ceny jako $T_{L}$ ).
Stejně pro $T_{R}$ .
Pak ale cena vrácená BVSOPT_rec je nanejvýš taková jako je cena $T$ .

Histogramové BVS - memoizace

Indexy $l, u \in n$ – odkud kam sahají aktivní data.
Pomocné pole $M [n] [n]$ incializované na $⊥$ .

Algoritmus 10.11 (BVSOPT)

 BVSOPT(ℓ, u)
    Pokud (M[ℓ, u] ̸= ⊥): Vrať M[ℓ, u]
    Pokud (ℓ > u): Vrať M[ℓ][u] := 0
    x := Sum(i=ℓ to u, p_i)
    m := +∞
    Pro každé r ∈ {ℓ, . . . , u}:
        c_L := BVSOPT(ℓ, r − 1)
        c_R := BVSOPT(r + 1, u)
        m := min(m, c_L + c_R)
    Vrať M[ℓ][u] := m + x    

Lemma o časové složitosti BVSOPT

BVSOPT(1, n) počítá v čase $O (n^{3})$ .

K zamyšlení

Časová složitos se dá vylepšit na $O (n^{2})$ pomocí chytřejšího výběru kořenu (řádek 6)