10.3 Nejdelší roustoucí podposloupnost (LIS)

Vyřešíme nejdřív jednodušší problém DelkaNrpRec(i):
- Pro dané \(i\) vrátí délku NRP začínající právě prvkem \(x_i\).
Postupně projdeme všechna \(x_j\) potenciálně navazující na \(x_i\).
Pro každé takové \(x_j\) zavoláme rekurzivně totéž
(čímž vypočítáme délku NRP začínající prvkem \(x_j\)).
Ze všech potenciálně navazujících prvků \(x_j\) si pak vybereme ten, který má svou NRP nejdelší a k délce jeho NRP přičteme jedničku.

Algoritmus 10.4 (DelkaNrpRec)

DelkaNrpRec(i)
    d := 1
    Pro j := i + 1,..., n:
        Pokud x_j > x_i:
            d := max(d, 1 + DelkaNrpRec(j))
Vrať d

Lemma o časové složitosti DelkaNrpRec

Časová složitost DelkaNrpRec(0) je \(O(2^n)\).

Důkaz časové složisti DelkaNrpRec

Struktura SRV závisí na velikostech prvků vstupní posloupnosti, protože se rekurze volá pouze pro potenciálně navazující prvky.
Nejvíce se rekurze volá v případě monotonně rostoucí posloupnosti a pak má SRV tvar binomiálního stromu \(B_n\)
V obecném případě je SRV podstromem \(B_n\)

Délku NRP celé vstupní posloupnosti získáme tak, že zavoláme DelkaNrpRec(i) postupně pro \(i = 1,\dots, n\) a vezmeme maximum z výsledků.
Elegantnější je ale dodefinovat \(x_0 = -\infty\), zavolat pouze DelkaNrpRec(0) a odečíst z výsledku jedničku, neboť \(x_0\) se bude v optimálním řešení NRP vždy zaručeně vyskytovat.

Délka NRP - memoizace

Pro snížení časové složitosti použijeme opět techniku memoizace.
Zavedeme tabulku \(T[0,\dots, n]\), na počátku prázdnou.
Na konci má být v \(T[i]\) uložena délka nejdelší ze všech rostoucích podposloupností začínajících prvkem \(x_i\).

Algoritmus 10.5 (DelkaNrpMem)

DelkaNrpMem(i)
    Pokud je T[i] definováno: Vrať T[i]
    T[i] := 1
    Pro j := i + 1,..., n:
        Pokud x_j > x_i:
            T[i] := max(T[i], 1 + DelkaNrpMem(j))
    Vrať T[i]

Lemma o časové složitosti DelkaNrpMem

Funkci DelkaNrpMem můžeme zavolat pouze pro \(n + 1\) různých argumentů.
Pokaždé v ní strávíme čas \(O(n)\), takže celkový čas je \(O(n^2)\).

Délka NRP - iterace

Pokud začneme vyplňovat tabulku v opačném směru od největšího \(i\) k nejmenšímu, rekurze se můžeme zbavit úplně.

Algoritmus 10.6 (DelkaNrpIter)

DelkaNrpIter(x1,...,xn)
    x_0 := −∞
    Pro i := n, n − 1,...,0:
        T[i] := 1
        Pro j := i + 1,...,n:
            Pokud x_i < x_j a T[i] < 1 + T[j]:
                T[i] := 1 + T[j]
    Vrať T[0] − 1

Pozorování

DelkaNrpIter má kvadratickou časovou složitost.

Pozorování

Algoritmus se dá vylepšit (řádky 4 - 6) za pomocí augmentace AVL stromu
a dostat se na složitost \(O(n \cdot log(n))\)

Lemma o korektnosti DelkaNrpIter

Po skončení DelkaNrpIter je v \(T[i]\) uložena délka nejdelší ze všech rostoucích podposloupností začínajících prvkem \(x_i\).

Důkaz korektnosti DelkaNrpIter

Zpětnou indukcí podle \(i\), tj. od \(n\) k 1.
Pokud je na konci \(T[i] = 1\), je \(x_i\) maximem v \(x_i,\dots, x_n\).
Pokud \(T[i]\) vzniklo jako \(1 + T[j]\) a tedy optimální řešení pro \(X = x_i,\dots, x_n\) začíná dvojicí \(x_i\), \(x_j\), pak z něj odebráním \(x_i\) vznikne optimální řešení pro kratší vstup \(X' = x_j,\dots, x_n\) začínající \(x_j\), jehož délka je v \(T[j]\).
Sporem: Kdyby existovalo lepší řešení pro kratší vstup \(X'\), mohli bychom ho rozšířit o \(x_i\) a získat lepší řešení pro původní \(X\).

Konstrukce NRP - iterace

Během výpočtu délky NRP si stačí při každém nalezení lepšího řešení zapamatovat i příslušný navazující prvek.

Algoritmus 10.7 (NrpIter)

NrpIter(x_1,...,x_n)
    x_0 := −∞
    Pro i := n, n − 1,...,0:
        T[i] := 1
        N[i] := ⊥
        Pro j := i + 1,...,n:
            Pokud x_i < x_j a T[i] < 1 + T[j]:
                T[i] := 1 + T[j]
                N[i] := j

nrp_iter

Lemma

NRP je po skončení výpočtu NrpIter podposloupnost s indexy \(N[0], N[N[0]], N[N[N[0]]],\dots\)

Důkaz koreknosti NrpIter

Kdykoliv se našlo větší \(T[i]\), uložil se do \(N[i]\) index druhého prvku příslušné delší rostoucí podposloupnosti začínající prvkem \(x_i\).
Po skončení proto \(N[0]\) říká, jaký prvek je v optimálním řešení celé úlohy první, N[N[0]] udává druhý a tak dále.
Pokud \(N[i] = \bot (nil)\), pak xi je maximem v \(x_i,\dots,x_n\) a každá případná rostoucí podposloupnost zde končí.
Pokud existuje více řešení, NrpIter vrátí to, které začíná nejvíce vlevo.

NRP - Grafový pohled

Ukažme si, že konstrukci NRP lze formulovat jako grafový problém.
Sestrojíme orientovaný graf \(G\), kde
- vrcholy jsou prvky \(x_0,\dots,x_{n+1}\), kde dodefinujeme \(x_0 = −\infty\) a \(x_{n+1} = +\infty\)
- \(x_i\) vedou hrany do potenciálně navazujících vrcholů \(x_j\) (pro které platí \(j > i\) a \(x_j > x_i\)),

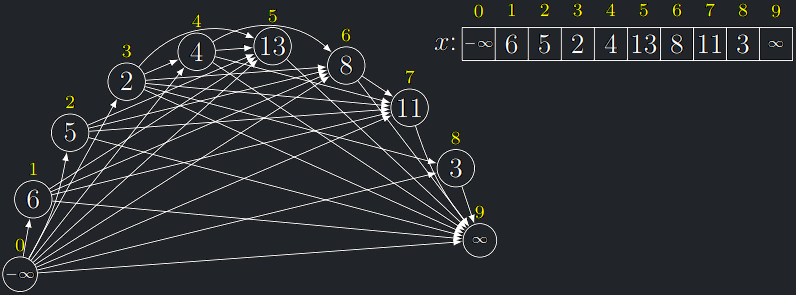
nrp_graph

Každá rostoucí podposloupnost odpovídá nějaké orientované cestě v \(G\).
Konstrukce NRP je tedy ekvivalentní nalezení nejdelší orientované cesty, která začíná v \(x_0\) a končí v \(x_{n+1}\).
\(G\) má \(\Theta(n)\) vrcholů a \(O(n^2)\) hran.

Pozorování

\(G\) je acyklický orientovaný graf a pořadí vrcholů \(x_0,\dots,x_{n+1}\) je jeho topologické uspořádání.

Nejdelší cestu v \(G\) pak nalezneme v čase \(O(n^2)\) algoritmem velmi podobným algoritmu NrpIter:
- Procházíme pozpátku topologickým uspořádáním \(x_n,\dots,x_0\).
- Pro každé \(x_i\) sestrojíme nejdelší cestu z \(x_i\) do \(x_{n+1}\) tak, že projdeme všechny hrany
  (\(x_i\), \(x_j\)) \(\in E(G)\) a vybereme takového souseda \(x_j\) , jehož cesta do \(x_{n+1}\) je nejdelší.
To je poměrně typické: DP je často ekvivalentní s hledáním cesty (či s jiným problémem) ve vhodném grafu.