Skip to content

10.2 Výpočet Fibonacciho čísla

Algoritmus 10.1 (FibRec)

1
2
3
FibRec(n)
    Pokud n ≤ 2: Vrať 1
    Jinak: Vrať FibRec(n − 1) + FibRec(n − 2)

Pozorování

Časová složitost volání funkce FibRec(n) je \(\Theta(F(n))\), kde \(F(n)\) je \(n\)-té Fibonacciho číslo,
tedy \(\Theta(\Phi^{n+1})\), kde \(\Phi \approx 1,61\) je hodnota zlatého řezu.

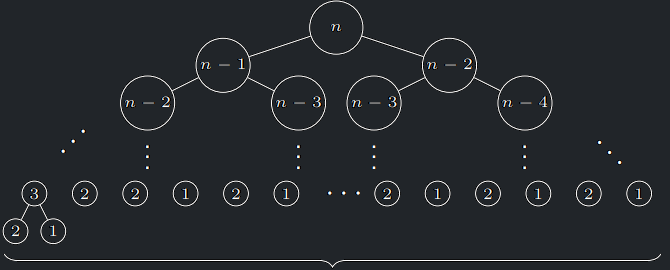
Důkaz časové složitosti FibRec
  • Ve stromu rekurzivních volání (SRV) je každý vrchol buďto list nebo vnitřní vrchol s přesně 2 syny (SRV je plný binární strom).
  • Počet vnitřních vrcholů je tedy nejvýše počet listů.
  • Libovolný vnitřní vrchol vrací součet hodnot ze svých synů, neboli součet hodnot všech listů ležících pod ním.
  • Každý list přitom vrací hodnotu 1.
  • Celkem tedy SRV obsahuje přesně \(F(n)\) listů.

strom rekurzivního volání

Výpočet Fibonacciho čísla - memoizace

  • Použijeme tabulku \(T\), na počátku obsahující nedefinované hodnoty.
  • Hodnotu \(F(i)\) zapíšeme do \(T[i]\), jakmile na ni při provádění rekurzivního algoritmu poprvé narazíme a poprvé ji vypočteme.
  • Při každém rekurzivním volání se nejdřív podíváme do políčka \(T\), odpovídajícího danému podproblému, zda již neobsahuje dříve vypočtené řešení.
  • Pokud ano, rekurzi nevoláme a vezmeme hodnotu z tabulky.
  • Pokud ne, voláme rekurzi.
  • Této technice se říká memoizace.

Algoritmus 10.2 (FibMem)

1
2
3
4
5
FibMem(n)
    Pokud je T[n] definováno: Vrať T[n]
    Pokud n ≤ 2: T[n] := 1
    Jinak: T[n] := FibMem(n − 1) + FibMem(n − 2)
    Vrať T[n]

Pozorování

Časová složitost volání funkce FibMem(n) je \(O(n)\).

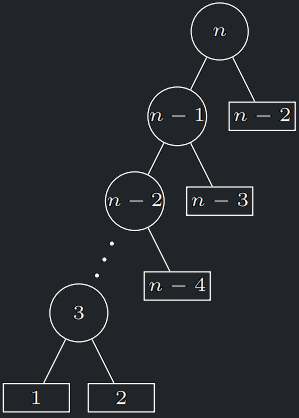
Důkaz časové složitosti FibMem
  • K rekurzivnímu volání nyní dojde jedině tehdy, vyplňujeme-li dosud nedefinované políčko tabulky.
  • Protože na počátku jsou všechna políčka prázdná, stane se toto \(n\)-krát, z toho dvakrát triviálně pro \(F(1)\) a \(F(2)\).
  • SRV má tedy \(n − 2\) vnitřních vrcholů a tedy \(n − 1\) listů.
  • Celkem tedy \(O(n)\) vrcholů, kde v každém strávíme \(O(1)\) čas

strom rekurzivního volání

Výpočet Fibonacciho čísla - iterace

  • Všimněme si ale, že pokud tabulku \(T\) budeme vyplňovat od nejmenších hodnot k největším, vůbec rekurzi nepotřebujeme a stačí jednoduchá iterace. (topologické uspořádání)

Algoritmus 10.3 (FibIter)

1
2
3
4
5
6
FibIter(n)
    T[1] := 1
    T[2] := 1
    Pro k := 3,..., n:
    T[k] := T[k − 1] + T[k − 2]
    Vrať T[n]

Pozorování

FibIter(n) funguje korektně a má časovou složitost \(O(n)\).