Skip to content

9.4 Dolní meze řazení

Dolní mez složitosti řazení v porovnávacím modelu

Definice 9.3 (Problém řazení)

Problém řazení

  • Vstup: Číslo \(n\) a posloupnost čísel \(A = a_{1}, a_{2}, . . . , a_{n}\).
  • Výstup: Taková permutace \(A^{′} = a_{1}^{′}, a_{2}^{′}, . . . , a_{n}^{′}\) vstupní posloupnosti A,
    že platí \(a_{1}^{′} \leq a_{2}^{′} \leq ... \leq a_{n}^{′}\)
  • Podobně jako u vyhledávání, si v porovnávacím modelu odvodíme těsnou dolní mez složitosti problému řazení.
  • Tedy asymptoticky nepodkročitelnou složitost řešení, kterou ale některé známé algoritmy (HeapSort, MergeSort, QuickSort) asymptoticky dosahují, a jsou tedy optimální

Definice 9.4 (Invariant)

Invariant

Invariant je podmínka v algoritmu, která musí být splněna po celou dobu běhu programu.

Příklad invariantu

1
2
3
4
5
int i = 0;
while( i < 10 ) {
    i++;
}
// i = 10

Invariantem zde je podmínka \(0 \le i \le 10\)

Dolní mez složitosti řazení

  • Pro účel stanovení dolní meze předpokládáme speciální typ vstupní \(n\) prvkové posloupnosti, a to permutaci množiny \(\{1, . . . , n\}\)
  • Problém řazení je z pohledu teorie informace ekvivalentní problému rozpoznání, o kterou permutaci z \(n!\) možných se na vstupu jedná.
  • Různé vstupní permutace je přitom třeba řadit různými posloupnostmi porovnání a prohození.
  • Víme, že \(e \cdot \frac{n^{n}}{e^{n}} \leq n! \leq en \cdot \frac{n^{n}}{e^{n}}\) (viz BI-DML – Stirlingova formule).
  • Počet potřebných bitů pro rozpoznání permutace, a tím pádem i potřebných porovnání, tedy musí být \(log(n!) \geq log(e \cdot \frac{n^{n}}{e^{n}}) = log e + n \cdot (log n − log e) = \Omega (n \cdot log n)\)
  • Stanovit dolní mez složitosti řazení ale můžeme pomocí rozhodovacích stromů podobně jako u problému vyhledávání.

Věta 9.5 (o složitosti řazení)

Věta o složitosti řazení

Každý deterministický algoritmus v porovnávacím modelu RAM, který seřadí \(n\)-prvkovou posloupnost, použije v nejhorším případě \(\Omega(n \cdot log n)\) porovnání.

Důkaz věty 9.5
  1. Zvolme pevné \(n\) a uvažujme vstupy \(A = a_{1}, . . . , a_{n}\), které jsou permutacemi množiny \(\{1, . . . , n\}\)
  2. Ukážeme, že pro libovolný řadicí algoritmus \(S\) v porovnávacím modelu RAM existuje „těžký“ vstup \(A\), který „donutí“ \(S\) provést \(\Omega (n \cdot log n)\) porovnání.

  3. Upravíme \(S\) tak, aby nejprve prováděl všechna porovnání a teprve na konec prvky přeindexoval.

    • Každý prvek si tedy pouze pamatuje průběžně novou pozici a na výslednou pozici se přesune až nakonec.

  4. Sestrojíme rozhodovací strom \(T_{S}\) popisující všechny možné průběhy algoritmu \(S\), tedy běhy pro všechny možné permutace.

  5. Vnitřní vrcholy \(T_{S}\) jsou porovnání cmp(\(a_{i}\), \(a_{j}\) ) se dvěma možnými výsledky (rovnost tentokrát nenastane díky volbě vstupní posloupnosti).
  6. Vynecháme výsledky, které jsou ve sporu s předchozími porovnáními.
  7. V listu stromu algoritmus S provede napočítané prohození a zastaví se.
  8. Pro různé vstupní permutace \(A\) musí algoritmus \(S\) skončit v různých listech \(T_{S}\) (dvě různé permutace nelze seřadit toutéž posloupností přesunů prvků).
  9. \(T_{S}\) je tedy binární zakořeněný strom s \(n!\) listy, takže musí mít hloubku nejméně \(log(n!)\), tedy \(\Omega(n \cdot log n)\)
  10. Proto musí existovat vstupní permutace A, pro kterou S provede \(\Omega(n \cdot log n)\) porovnání

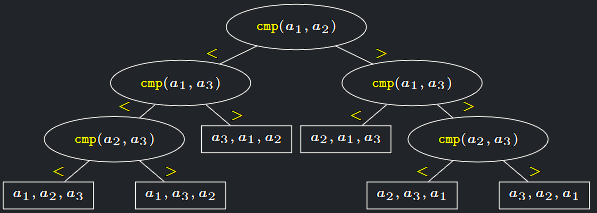
Image title

Příklad rozhodovacího stromu TS pro nějaký algoritmus S a n = 3

Dolní meze složitosti dalších operací

Důsledek

Každá korektní implementace operace ExtractMin v binární haldě (taková, že po provedení ExtractMin bude struktura splňovat podmínky haldy) s \(n\) prvky musí mít časovou složitost \(\Omega(log n)\) v nejhorším případě.

Důkaz

Sporem:

  1. Předpokládejme, že existuje algoritmus ExtractMin, který má v nejhorším případě časovou složitost \(O(f (n))\), kde \(f (n) = o(log n)\)
  2. Mějme prvky \(a_{1}, . . . , a_{n}\) a uložme je do pole P
  3. Na toto pole zavolejme funkci HeapBuild, která z něj v čase \(O(n)\) vytvoří korektní binární haldu.
  4. Potom zavolejme \(n\)-krát funkci ExtractMin, čímž vypíšeme seřazenou posloupnost.
  5. Dostáváme tím algoritmus, který seřadí n čísel v celkovém čase \(n \cdot O(f (n)) = o(n log n)\)
  6. To je ale spor s předchozí větou o složitosti problému řazení, která dokazuje, že takový algoritmus neexistuje.