9.3 Dolní meze vyhledávání

• Nacházení dolních mezí složitosti různých problémů jsou obecně obtížná.

• Dolní meze složitosti si v této přednášce ukážeme na dvou problémech:

  • problém vyhledávání v seřazené číselné posloupnosti a
  • problém řazení neseřazené číselné posloupnosti.

• Dolní meze složitosti budeme určovat za následujících předpokladů:

  • Algoritmy pracují v porovnávacím modelu RAM, kde smějí vstupní prvky pouze vzájemně porovnávat a případně přesouvat.
  • Porovnání cmp(\(a_{i}\), \(a_{j}\) ) je binární operace, která v konstantním čase pro dva prvky \(a_{i}\) a \(a_{j}\) odpoví, zda platí \(a_{i} \lt a_{j}\) , \(a_{i} = a_{j}\) nebo \(a_{i} \gt a_{j}\)
  • Uvažujeme pouze deterministické algoritmy, které nepoužívají žádný zdroj náhody a jejichž každý krok je jednoznačně určen výsledky kroků předchozích.

Dolní mez složitosti vyhledávání

Definice 9.2 (Problém vyhledávání v seřazené posloupnosti)

Problém vyhledávání v seřazené posloupnosti

• Vstupem algoritmu je číslo \(n\), vzestupně seřazená posloupnost \(A\) \(n\) čísel \(a_{1}, . . . , a_{n}\) a hledané číslo \(x\)
• Úkolem algoritmu je zjistit, zda se \(x\) vyskytuje v \(A\)

Věta 9.4 (o složitosti vyhledávání)

Věta o složitosti vyhledávání

Každý deterministický algoritmus v porovnávacím modelu RAM, který řeší problém vyhledávání v seřazené posloupnosti, použije v nejhorším případě \(\Omega (log n)\) porovnání.

Jinými slovy: žádný deterministický algoritmus v porovnávacím modelu RAM nemůže v nejhorším případě nalézt dané číslo v \(n\)-prvkové seřazené posloupnosti použitím \(o(log n)\) operací porovnání. To ale znamená, že známé binární vyhledávání s \(O(log n)\) srovnáními je optimální algoritmus pro vyhledávání.

Důkaz věty 9.4

1. Dokážeme, že pro libovolný deterministický vyhledávací algoritmus \(S\) a pro libovolné n a pro libovolnou vstupní vzestupně seřazenou posloupnost \(A = a_{1} \lt a_{2} \lt · · · \lt a_{n}\) existuje \(x\) takové, že algoritmus \(S\) při hledání \(x\) v posloupnosti \(A\) provede \(\Omega (log n)\) porovnání.
2. První porovnání, které algoritmus \(S\) se vstupem \(A\) provede, bude vždy stejné, neboť je deterministický.
3. Porovnání typu cmp(\(a_{i}\), \(a_{j}\) ) dopadne také vždy stejně.
4. Až první porovnání typu cmp(\(x\), \(a_{i}\)) může pro různá vstupní \(x\) dopadnout různě.
5. Pro každý z možných výsledků tohoto porovnání pokračuje \(S\) deterministicky, takže algoritmem \(S\) je pevně dáno, které další porovnání se provede.
6. A tak dále, až se \(S\) zastaví s výsledkem buď \(x \in A\) nebo \(x \notin A\)

7. Protože \(S\) je deterministický algoritmus, můžeme jeho provedení se vstupem \(A\) pro všechna možná \(x\) popsat takzvaným rozhodovacím stromem \(T_{S,A}\)

   • Každý vnitřní vrchol rozhodovacího stromu \(T_{S,A}\) je porovnání typu cmp(\(x\), \(a_{i}\)) a má tedy obecně tři syny, kteří odpovídají možným výsledkům tohoto porovnání (<, =, >).
   • Může se stát, že některý z výsledků nemůže vzniknout, protože by byl ve sporu s dříve provedenými porovnáními. V takovém případě příslušný syn neexistuje (je prázdný).
   • V listech \(T_{S,A}\) jsou jednotlivé výsledky hledání: buď pozice v \(A\), na které se \(x\) vyskytuje, nebo odpověď, že \(x\) v \(A\) neexistuje. Každé možné provedení algoritmu \(S\) se vstupem \(A\) pro nějaké \(x\) odpovídá nějaké cestě z kořene \(T_{S,A}\) do listu.

8. Rozhodovací strom \(T_{S,A}\) je tedy ternární (vrcholy mají nejvýše 3 syny) s nejméně \(n + 1\) listy (lze dokázat, že má alespoň \(2n + 1\) listů, ale my si vystačíme s \(n + 1\) listy).

9. Protože každý ternární strom hloubky \(h\) má nejvýše \(3^{h}\) listů, má \(T_{S,A}\) hloubku nejméně \(log_{3}n\).
10. V \(T_{S,A}\) tedy existuje cesta délky nejméně \(log_{3}n\) a proto existuje \(x\), které této cestě odpovídá.
11. A takové \(x\) „donutí“ \(S\) vykonat nejméně \(log_{3}n\) porovnání

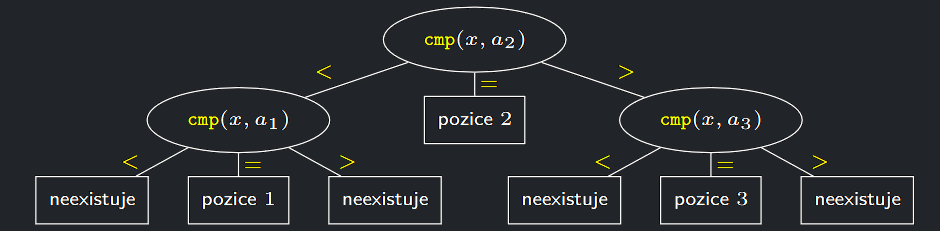
Příklad rozhodovacího strom \(T_{S,A}\) pro nějaký algoritmus \(S\) a nějaký vstup \(A\) délky \(n = 3\)