9.2 Složitost quicksortu
I. Správná volba pivotu
Pokud za pivoty volíme mediány nebo alespoň skoromediány, pak:
- Velikosti podproblémů klesají exponenciálně: na \(i\)-té hladině SRV je velikost většího z \(L \text{ , } P\) nejvýše \((\frac{3}{4})^{i} · n\)
- SRV má tudíž hloubku \(O(log_{\frac{4}{3}} n) = O (logn)\)
- V součtu přes všechny hladiny proto časová složitost činí \(O(n log n)\)
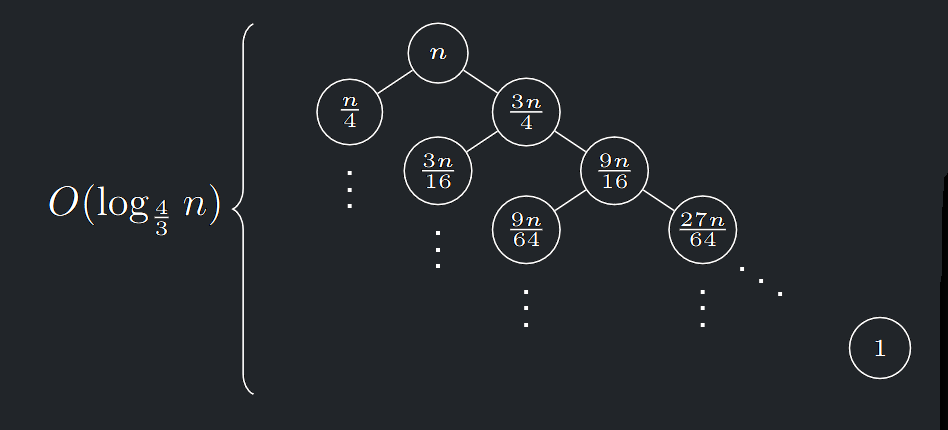
Složitost při správné volbě pivotu
II. Špatná volba pivotu
Jestliže naopak volíme tím nejhorším způsobem, např. jako minima podposloupností na každé hladině SRV, pak:
- Se na každé hladině oddělí od vstupu jen úsek o jednom prvku
- Hladin bude \(\Theta (n)\)
- To povede na kvadratickou časovou složitost.
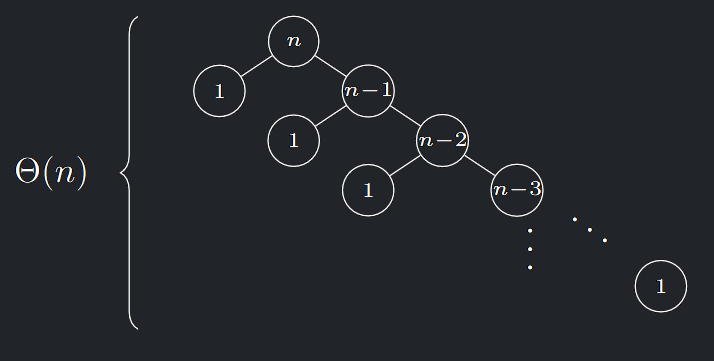
Složitost při špatné volbě pivotu
Analýza časové složitosti QuickSortu s náhodnou volbou pivota
- Zanalyzujeme nyní variantu QuickSortu, ve které budeme v každé fázi volit pivota náhodně jako jeden z prvků na vstupu.
- To uděláme podobně jako u QuickSelectu
Pozorování
QuickSort porovná jednu dvojici prvků nejvýše jednou. Na každé porovnání provede QuickSort pouze \(O(1)\) dalších operací. Proto pro řádový odhad jeho složitosti postačí odhadnout počet provedených porovnání.
Věta 9.1 (o složitosti QuickSortu s náhodnou volbou pivota)
Věta o složitosti QuickSortu s náhodnou volbou pivota
Střední hodnota časové složitosti QuickSortu s rovnoměrně náhodnou volbou pivota je \(O(n log n)\)
Definice 9.1 (Indikátory)
Indikátory
Náhodným veličinám, které nabývají hodnoty 0 nebo 1 podle toho, zda nějaká událost nastala, se obvykle říká indikátory.
Pro střední hodnotu indikátoru \(X\) tedy platí:
Příklad
Vezměme náhodné \(b\)-bitové binární číslo. Pro \(i\)-tý bit zavedeme náhodnou proměnnou \(X_{i}\), nabývající hodnoty tohoto bitu.
Potom \(E[X_{i}] = \frac{1}{2}\) a \(E[X] = E[X_{1} + · · · + X_{b}] = \frac{b}{2}\)
Lemma (součet harmonické řady)
Pro součet harmonické řady \(H_{n} = \frac{1}{1} + \frac{1}{2} + · · · + \frac{1}{n}\) platí \(H_{n} = \Theta(log n)\)
Důkaz (viz. BI-MA1)
a víme, že \(ln(n) = \Theta(log n)\).
Důkaz věty o analýze QuickSortu – shrnutí
- Vstupní posloupnost \(X = x_{1}, x_{2}, . . . , x_{n}\)
- Výstupní posloupnost \(Y = y_{1}, . . . , y_{n}\) - tedy seřazená posloupnost
Budeme určovat střední počet porovnání v průběhu Quicksort
- Protože pivota volíme náhodně, je porovnání \(y_{i}\) s \(y_{j}\) náhodný jev. Pro \(1 \leq i \lt j \leq n\) zavedeme náhodné veličiny \(C_{ij}\) takto:
Poté určíme, že:
Tím bude důkaz hotov.
Lemma
Pro \(1 \leq i \lt j \leq n\) platí \(E[C_{ij} ] = P[Cij = 1] = \frac{2}{(j − i + 1)}\)
Důkaz
- Určeme pravděpodobnost porovnání \(y_{i}\) s \(y_{j}\) , čili \(P[C_{ij} = 1]\)
- QuickSort porovnává prvky pouze s pivotem, takže jeden z prvků \(y_{i}\), \(y_{j}\) se těsně před porovnáním musí stát pivotem.
- Současně ale žádný prvek z \(y_{i+1}, . . . , y_{j−1}\) ještě pivotem být nemohl, jinak by \(y_{i}\) a \(y_{j}\) patřily do různých částí posloupnosti a nemohly by být porovnány.
- Jinými slovy, \(C_{ij} = 1\) právě tehdy, když se z prvků \(y_{i}, y_{i+1}, . . . , y_{j}\) stane pivotem jako první buď \(y_{i}\) nebo \(y_{j}\)
- Protože pivota vybíráme náhodně, může být každý z prvků \(y_{i}, . . . , y_{j}\) vybrán se stejnou pravděpodobností \(\frac{1}{(j − i + 1)}\)
- Proto \(P[C_{ij} = 1] = \frac{2}{(j − i + 1)}\)
Důkaz věty o analýze QuickSortu
Důkaz věty o analýze QuickSortu
Definujme náhodnou veličinu \(C\) jako celkový počet všech porovnání provedených během běhu QuickSortu
Pak \(C = \sum_{1 \leq i \lt j \leq n}{C_{ij}}\)
Pro střední hodnotu celkového počtu porovnání provedených během běhu QuickSortu tak dostaneme:
substitucí \(j − i = d\), čili \(1 \leq d \leq n − 1, i \geq 1\) a \(i \leq n − d\), a tedy:
Na odhad poslední sumy nyní použijeme lemma o součtu harmonické řady, tedy:
Složitost QuickSortu v průměru přes vstupy
- Pokud se bere pivot z pevné pozice (např. prostřední prvek), není QuickSort odolný proti zlomyslnému uživateli, který umí konstruovat vstupní posloupnosti, kde na tyto pozice dává nejhorší pivoty (např. minima) a vnutí kvadratickou složitost.
- Bez důkazu uveďme, že i pro pevnou volbu pivota je ale "špatných" vstupů (vedoucích na \(\omega (n \cdot log n)\) složitost) málo
- Již jsme si vysvětlili, že tomu se vyhneme náhodnou volbou pivota, tedy randomizací
- Stejně jako v minulé přednášce u QuickSelectu, můžeme i pro QuickSort zavést složitost v průměru přes vstupy
- QuickSort bude deterministicky vybírat pivota z pevné pozice.
- Na vstup mu ale budeme dávat náhodné posloupnosti a budeme počítat, jak dlouho v průměru poběží.
Deterministický QuickSort s náhodnými vstupy
Věta 9.3 (o střední hodnotě počtu operací quicksortu)
Věta o střední hodnotě počtu operací quicksortu
Uvažujme na vstupu rovnoměrně náhodné permutace \(\{1, . . . , n\}\) Jako pivota volíme vždy prvek např. na prostřední pozici. Potom střední hodnota počtu operací vykonaných při jednom běhu QuickSortu je \(O(n \cdot log n)\)
Hlavní myšlenka důkazu
Vzhledem k náhodnosti vstupu je prostřední prvek rovnoměrně náhodně vybrané číslo z množiny \(\{1, 2, . . . , n\}\) Lze tedy použít obdobnou analýzu jako ve Větě o složitosti QuickSortu s náhodnou volbou pivota.