8.3 Rekurzivní formulace násobení dvou celých čísel
- Ukážeme nejprv, že i násobení celých čísel lze popsat rekurzivně.
- Mějme dvě \(n\)-ciferná čísla \(x\) a \(y\), která chceme vynásobit.
- Pro jednoduchost zatím předpokládejme, že \(n\) je mocnina dvou.
- Obě čísla rozdělíme na horních \(n/2\) a dolních \(n/2\) cifer. Platí tedy
\(x = x_U \cdot 10^{n/2} + x_L,\)
\(y = y_U \cdot 10^{n/2} + y_L,\)
- kde \(x_U, x_L, y_U, y_L\) jsou (\(n/2\))-ciferná čísla.
- Výsledný součin dvou n-ciferných čísel \(xy\) pak můžeme poskládat ze 4 součinů \(n/2\) ciferných čísel:
\[x·y= x_U·y_U·10^n + (x_U·y_L + x_L·y_U)·10^{n/2} + x_L·y_L\]
- Rekurzivně tedy spočítáme 4 součiny dvojic čísel poloviční délky: \(x_U·y_U, x_U·y_L, x_L·y_U\) a \(x_L·y_L\).
- Výsledek z těchto dílčích součinů složíme pomocí několik \(2n\)-ciferných sčítání (sčítání má lineární složitost vzhledem k počtu cifer) a několika násobení mocninou desítky (doplňování nejvýše n nul na konec).
- Řešíme tedy čtyři podproblémy poloviční velikosti a pak provedeme několik operací s lineární složitostí vzhledem k n.
- Pro časovou složitost proto platí:
\(T (1) = 1\),
\(T (n) = 4·T (n/2) + Θ(n)\).
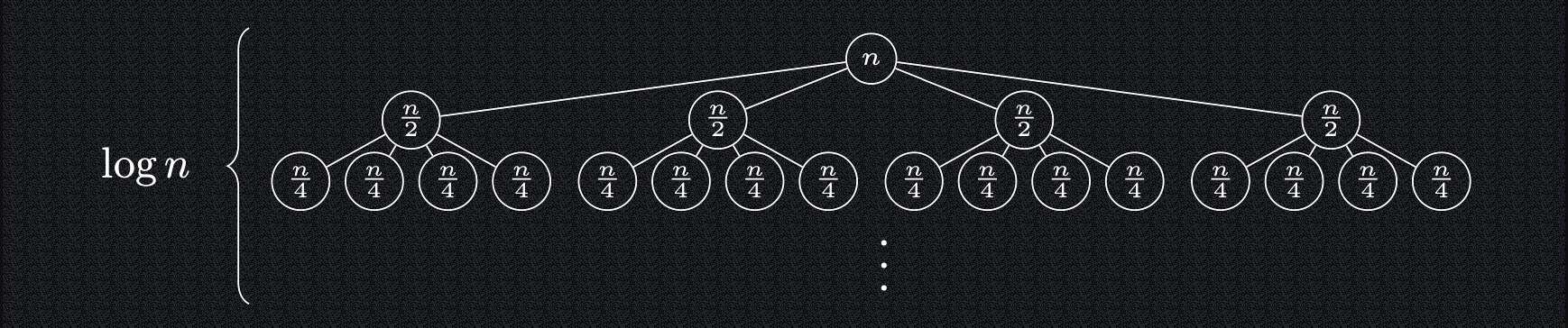
Strom rekurzivních volání násobení čísel
- Strom rekurzivních volání má následující vlastnosti:
- Na jeho \(i\)-té hladině se nachází \(4^i\) vrcholů, které reprezentují násobení dvou čísel o \(n/2^i\) cifrách.
- V každém vrcholu této hladiny tedy trávíme čas \(Θ(n/2^i)\) a na celé hladině \(4^i·Θ(n/2^i) = Θ(2^i·n)\).
- Jelikož hladin je opět \(log\ n\), strávíme jenom na poslední hladině čas \(Θ(2^{log\ n} ·n) = Θ(n^2)\).
- Čili \(T (n) = Θ(n^2)\) a oproti běžnému „školnímu“ násobení jsme si tedy nepomohli.
Vylepšené násobení čísel: Karacubův algoritmus
- Hlavní nápad rychlejšího násobení dvou čísel pomocí Karacubova algoritmu vychází z postřehu, že téhož efektu lze dosáhnout pomocí pouze 3 násobení čísel poloviční délky.
- Pro výpočet \((x_U·y_L + x_L·y_U)\) jsme potřebovali 2 násobení čísel poloviční délky.
- Triviálně platí \(x_U·y_L + x_L·y_U = (x_U + x_L)·(y_U + y_L)−x_U·y_U−x_L·y_L\)
- Rekurzivní způsob násobení lze tedy přepsat na tvar \(x·y=\)
\[x_U·y_U·10^n +((x_U +x_L)·(y_U +y_L)−x_U·y_U−x_L·y_L)·10^{n/2} +x_L·y_L\]
- Místo 4 násobení máme pouze 3 a přibyly 2 operace sčítání, ale ty mají pouze lineární složitost.
- Rekurzivní náhrada 1 nasobení dvěma sčítáními zmenší časovou složitost.
Věta 8.3
Časová složitost Karacubova algoritmu
Časová složitost Karacubova algoritmu je \(Θ(n^{\log_2{3}}) ≈Θ(n^{1,59})\).
Důkaz Věty 8.3
- Počet operací je \(T (1) = 1\),
- \(T (n) = 3·T (n/2) + Θ(n)\).
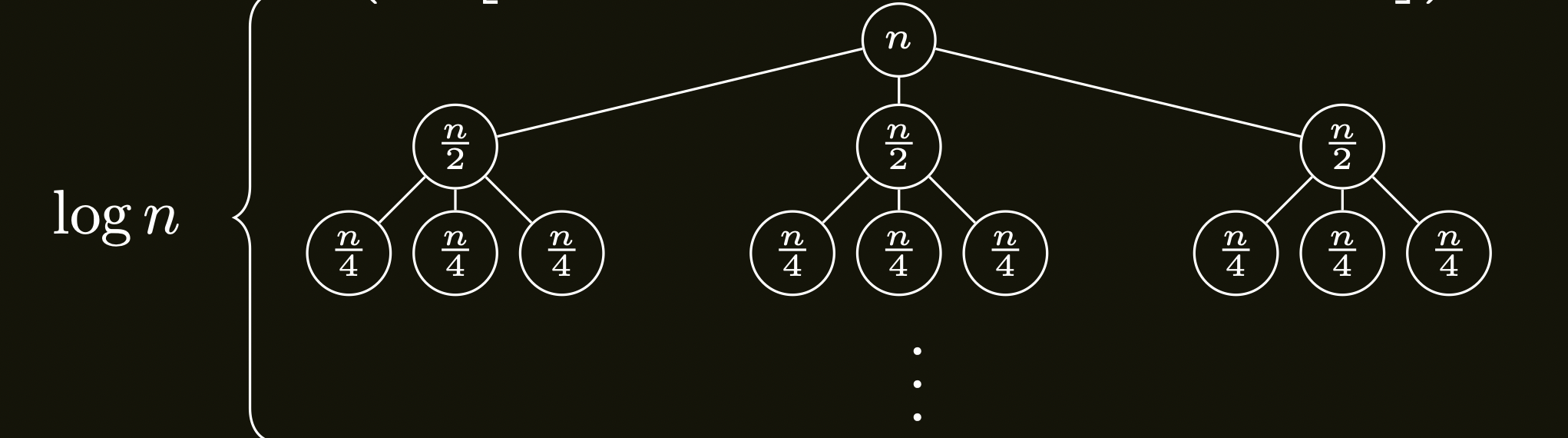
- Strom rekurzivních volání vypadá takto:
- Na \(i\)-té hladině je \(3^i\) vrcholů s (\(n/2^i\))-cifernými problémy.
- Na \(i\)-té hladině nyní dohromady trávíme čas \(Θ(n·(3/2)^i)\).
- Hloubka stromu se nezměnila a zůstává tedy nadále \(log\ n\).
- V součtu přes všechny hladiny dostaneme:
\(T (n) = Θ( n· [(3/2)^0 + (3/2)^1 +···(3/2)^{log\ n}])\)
. .
.
\(T (n) = Θ \left( n \cdot \left[ \left( \frac{3}{2}\right)^0 + \left(\frac{3}{2}\right)^1 + ... + \left(\frac{3}{2}\right)^{\log{n}} \right] \right)\) - Výraz v hranatých závorkách je geometrická řada s koeficientem \(\frac{3}{2}\)
- Tu můžeme sečíst obvyklým způsobem na \(\frac{ \left( \frac{3}{2}\right)^{1 + \log{n}} - 1}{\frac{3}{2} - 1}\)
- Když zanedbáme konstanty, obdržíme \((\frac{3}{2})^{\log{n}}\)
- To dále upravíme na \((2^{\log{\frac{3}{2}}})^{\log{n}} = 2^{\log{\frac{3}{2} \cdot \log{n}}} = (2^{\log{n}})^{\log{\frac{3}{2}}} = n^{\log{\frac{3}{2}}} = n^{\log{3} - 1}\)
- Časová složitost našeho algoritmu tedy činí \(Θ(n·n^{\log{3}−1}) = Θ(n^{\log{3}}) ≈Θ(n^{1,59})\).
Pseudokód Karacubova algoritmu pro obecné \(n\)
- Zatím jsme předpokládali, že n je mocnina dvou.
- Pro obecné, resp. liché \(n\), si ze dvou možností, jak dělit lichý počet cifer \(n\) na horní a dolní polovinu pozic, vybereme např. \(x = x_U·10^{⌈n/2⌉}+ x_L\) a \(y= y_U·10^{⌈n/2⌉}+ y_L\). Pak:
8.3 Karacubuv algoritmus