8.2 MergeSort

• Jedná se o rychlý rekurzivní algoritmus pro řazení, založený na slévání seřazených podposloupností.
• Posloupnost o jednom prvku je už seřazená.
• Mějme vstupní neseřazenou posloupnost \(n\) prvků pro \(n\) \(\geq 2\).
• Rozdělíme ji na dvě části poloviční délky (řekněme prvních \(⌊n/2⌋\) a zbývajících \(⌈n/2⌉\) prvků).
• Rekurzivním voláním téhož algoritmu na obě poloviny je seřadíme.
• Obě seřazené poloviny posléze slijeme dohromady do jedné seřazené posloupnosti a máme výsledek.

---

Vstup: posloupnost \(n\) čísel
Výstup: vzestupně seřazená posloupnost ze vstupu

---

Algoritmus 8.1 (Mergesort)

Pokud n = 1: vrať jako výsledek b1 = a1 a skonči
x1,..., x⌊n/2⌋:= MergeSort(a1,..., a⌊n/2⌋)
y1, ..., y⌈n/2⌉:= MergeSort(a⌊n/2⌋+1,..., an)
Vrať b1,..., bn := Merge(x1,..., x⌊n/2⌋; y1,..., y⌈n/2⌉)

• Procedura Merge má na vstupu dvě vzestupně seřazené posloupnosti (jednorozměrná pole) a provádí jejich slévání do jediné seřazené posloupnosti.
• Dostaneme tak datově necitlivý, out-of-place a stabilní řadící algoritmus.

---

Vstup: dvě vzestupně seřazené posloupnosti
Výstup: vzestupně seřazená posloupnost vzniklá slitím vstupů

---

Algoritmus 8.2 (Merge)

i := 1, j := 1, k := 1
Dokud i ≤ m a j ≤ n, opakujeme:
    Pokud xi ≤ yj :                             //přesuneme prvek z x
        zk := xi, i := i + 1 
    Jinak:                                      //přesuneme prvek z y
        zk := yj , j := j + 1
    k := k + 1
Pokud i ≤ m:                                     //přesuneme zbytek x
    zk,...,zm+n := xi,...,xm
Pokud j ≤ n:                                    //přesuneme zbytek y
    zk,...,zm+n := yj,...,yn
Vrať z1,...,zm+n

---

Příklad řazení pomocí algoritmu Mergesort

---

---

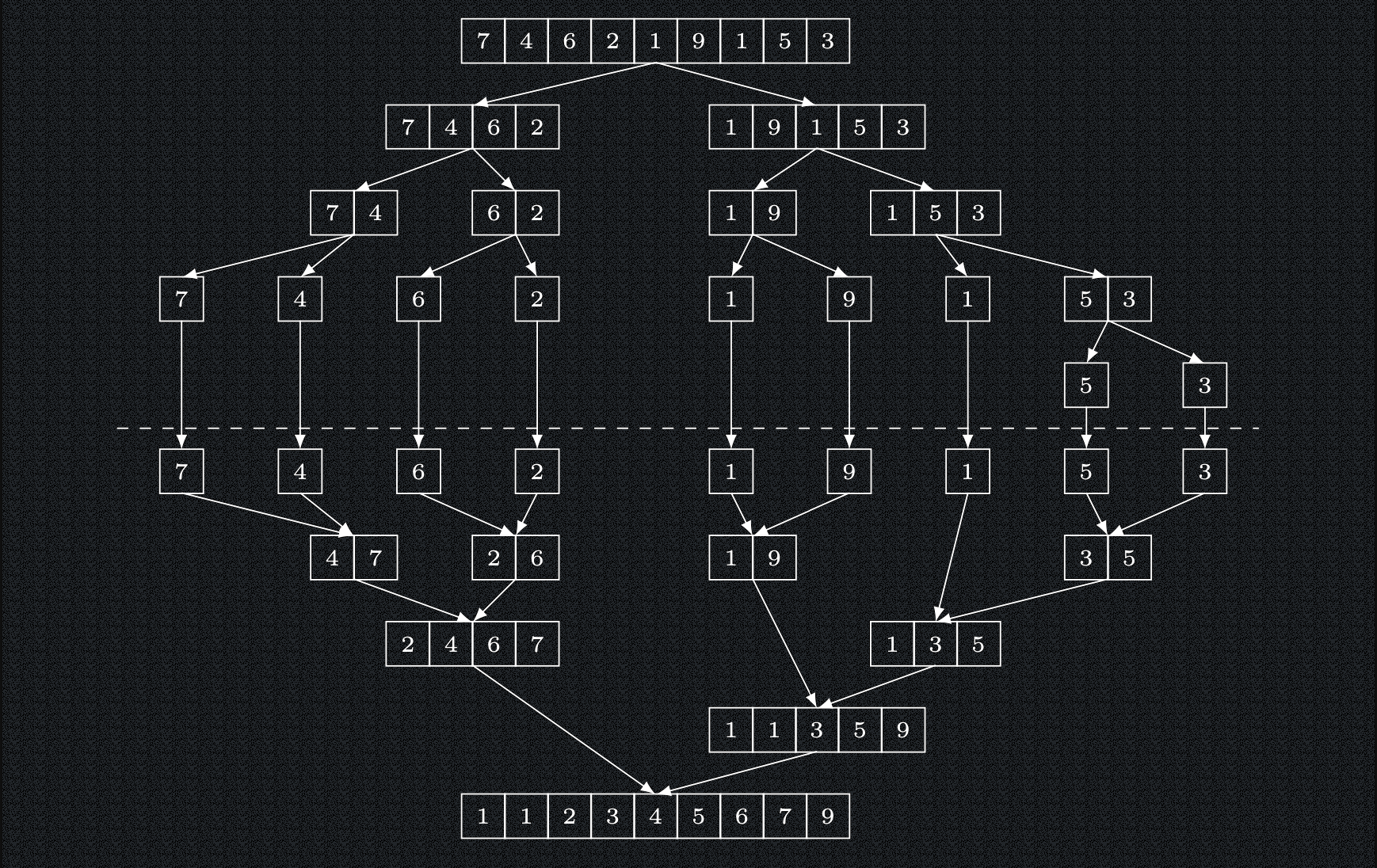
Časová složitost algoritmu MergeSort

---

Pozorování

• Operace Merge pouze přesouvá prvky a každý prvek přesune právě jednou.
• Její časová složitost je tedy \(Θ(n + m)\), kde \(n\), \(m\) jsou délky slévaných polí.
• Vyžaduje pomocnou paměť ve formě pomocného pole velikosti \(Θ(n + m)\).

Věta 8.1

Časová složitost MergeSort

Časová složitost MergeSort je \(Θ(n\ log n)\).

Důkaz Věty 8.1

• Rozdělení posloupnosti a slití seřazených kusů trvá čas \(cn\).
• Algoritmus volá \(2×\) sebe sama na vstupy velikosti \(n/2\). Proto
  \(T (1) = 1\),
  \(T (n) = 2·T (n/2) + cn\).
• Po rozvinutí dostaneme:
  \(T (n) = 2·(2·T (n/4) + cn/2) + cn =\)
  \(= 4·T (n/4) + 2cn =\)
  \(= 8·T (n/8) + 3cn =\)
  \(···\)
  \(= 2^k·T (n/2^k) + kcn.\)
• Rekurze skončí, když \(n/2^k = 1\) čili \(k = log\ n\). Tím dostaneme \(T (n) = 2^{log\ n}·T (1) + log\ n·cn = Θ(n) + cn\ log\ n = Θ(n\ log\ n)\).

Věta 8.2

Paměťová složitost MergeSort

Paměťová složitost MergeSort je \(Θ(n)\).

Důkaz Věty 8.2

• MergeSort si pamatuje lokální proměnné: vstup a jejich setříděné poloviny, dohromady \(Θ(n)\) paměti. Plus kontext pro návrat z rekurzivního zanoření (\(O(1)\) paměti).
• Mimo to obě rekurzivní volání spotřebují další paměť, ale jelikož vždy běží pouze jedno z nich, stačí započítat pouze jedno.
• Dostaneme tuto rekurentní rovnici (pro kladnou konstantu \(d\)):
  \(M (1) = 1\),
  \(M (n) = dn + M (n/2)\)
• To nám pro \(M (n)\) dává geometrickou řadu \(dn + dn/2 + dn/4 +···\), která má součet \(Θ(n)\).