7.3 Řešení kolizí

Jelikož \(m \ll |U|\), žádná hešovací funkce se nemůže vyhnout kolizím, kdy je několik prvků zahešováno do téže přihrádky.

Existují dvě principiálně odlišné metody řešení kolizí:

1. Řetězení (Chaining) = Otevřené hešování (Open hashing). Otevřené hešování proto, že ukládané prvky nejsou ukládány do hešovací tabulky, ale do „otevřeného prostoru“ za ní, do řetízků, odkazovaných z tabulky.

2. Otevřené adresování (Open addressing) = Uzavřené hešování (Closed hashing). Uzavřené hešování proto, že prvky jsou ukládány do „uzavřeného prostoru tabulky“. Otevřené adresování proto, že číslo (index) přihrádky tabulky, kam je nakonec hešovaný prvek uložen, je dopředu otevřený, neboť není dán pouze hešovací funkcí, ale i momentální obsazeností tabulky.

---

Řešení kolizí řetězením

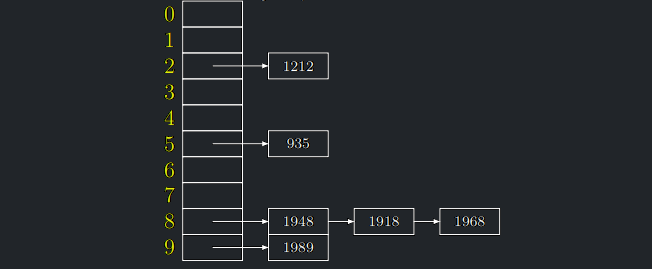
• Hešovací tabulka je pole \(m\) přihrádek, které jsou buď prázdné nebo obsahují ukazatel na řetízky (= spojové seznamy) uložených prvků.
• Jedná se o přímočarou implementaci abstraktní struktury hešovací tabulky.
• Naše tabulka bude tedy implementovaná takto:

Časová složitost hešování s řetízky

• Hledání, vkládání i mazání sestává z výpočtu hešovací funkce a projití řetízku v příslušné přihrádce.
• V případě ideální hešovací funkce a pokud jsou vstupní data z univerza \(\mathcal{U}\) vybírána nezávisle rovnoměrně náhodně, budou mít (skoro) všechny řetízky délku nejvýše \(\lceil n/m \rceil\) prvků.
• Zvolíme-li navíc počet přihrádek \(m = \Theta(n)\), vyjde konstantní délka řetízku, a tím pádem i časová složitost operací.

---

Otevřená adresace: Řešení kolizí

• Hešovací tabulka s otevřenou adresací je pole s \(m\) přihrádkami \(A[0],...,A[m − 1]\), jenže tentokrát se do každé přihrádky vejde pouze jeden prvek.
• Při pokusu o uložení do obsazené přihrádky budeme postupně zkoušet náhradní přihrádky, dokud nenajdeme prázdnou
• Hešovací funkce tedy každému klíči \(k \in \mathcal{U}\) přiřadí jeho vyhledávací posloupnost \(h(k,0),h(k,1),...,h(k,m − 1)\), která je ideálně permutací posloupnosti \(\{0,1,...,m − 1\}\).
• Ta určuje pořadí přihrádek, do kterých se budeme postupně snažit vkládat klíč \(k\).
• V ideálním případě vyhledávací posloupnost obsahuje všechna čísla přihrádek v dokonale náhodném pořadí (všechny permutace přihrádek jsou stejně pravděpodobné).

Find

Algoritmus 7.1 (Otevřená adresace: Hledání)

Algoritmus OpenFind

Pro i = 0,...,m − 1:
    j := h(k, i)
    Pokud k(A[j]) = k: ohlaš nalezení A[j] a skonči
    Pokud je A[j] prázdná: ohlaš neúspěch a skonči
Ohlaš neúspěch

Delete

• Mazání je problematické. Pokud bychom přihrádku smazaného prvku označili jako prázdnou, můžeme způsobit, že existující prvek s nějakým jiným klíčem \(k'\) nebude nalezen, protože vyhledávací posloupnost, která byla použita při vkládání \(k'\), bude tímto zásahem přerušena.

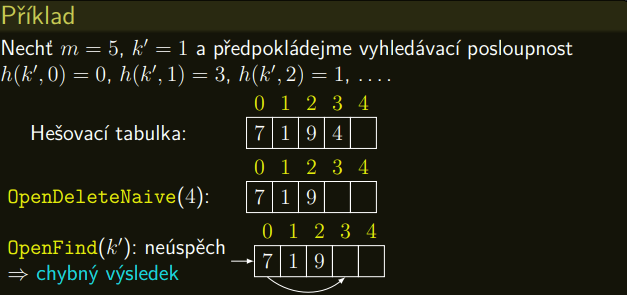
• Proto budeme mazané prvky pouze označovat za smazané.
• Standardní implementace označení smazaného prvku je pomocí tzv. náhrobku \(†\) (\(tombstone\)).
• Dodefinujeme \(k(†)\) jako libovolnou hodnotu mimo \(\mathcal{U}\).

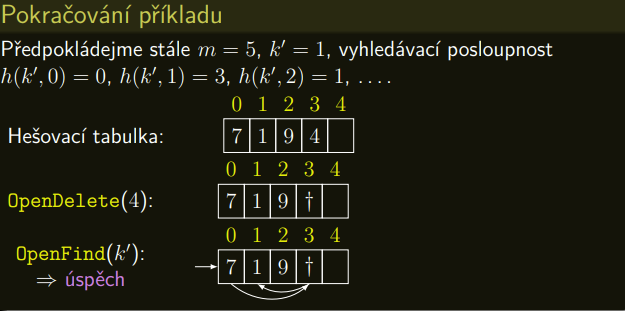
Algoritmus 7.2 (Otevřená adresace: Mazání)

Algoritmus OpenDelete

Idea

• Prvek nahradíme †.
• Operace OpenDelete je pak následující:

Pro i = 0, . . . , m − 1:
    j := h(k(x), i)
    Pokud je A[j] = x:
        A[j] = †
        skonči
    Pokud je A[j] prázdná:
        skonči

Insert

Algoritmus 7.3 (Otevřená adresace: Vkládání)

Algoritmus OpenInsert

Idea

• Místo po smazaných prvcích můžeme využívat při vkládání
• Operace OpenInsert je pak následující:

Pokud OpenFind(k(x)) nalezne k(x): skonči
Pro i = 0,...,m − 1:
    j := h(k(x),i)
    Pokud je A[j] prázdná nebo A[j] = †:
        A[j] := x a skonči
Ohlaš zaplnění hešovací tabulky

• Pokud se vyhledávací posloupnosti nově vkládaných prvků liší od vyhledávacích posloupností mazaných prvků označovaných náhrobky, počet náhrobků může snadno přesáhnout zadanou mez (třeba m/4). Pak se obvykle struktura tabulky přebuduje (přehešuje).