7.1 Slovníky a Hešovací tabulky

Slovníky

Nejjednodušší datovou strukturou pro práci s dynamickými množinami je slovník (tabulka, mapa, asociativní pole).

Definice 7.1 (Slovník)

Prvky slovníku jsou stejně jako v předchozích přednáškách dvojice (klíč,hodnota). Klíč prvku x značíme zase k(x).
Slovník je datová struktura, která umožňuje reprezentovat dynamickou podmnožinu prvků s klíči \(K \subseteq \mathcal{U}\), kde \(|K| \ll |\mathcal{U}|\), a efektivně podporovat operace
- Find(\(k\)): zjisti, zda prvek \(k \in K\) (příp. vrať hodnotu prvku).
- Insert(\(x\)): pokud \(k(x) \notin K\), vlož \(x\) do slovníku.
- Delete(\(x\)): pokud \(k(x) \in K\), vymaž \(x\) ze slovníku.

Prvky se tedy vyhledávají a ukládají podle svých klíčů.
Klíče jsou unikátní, t.j., v daném okamžiku se vyskytuje nejvýše jeden prvek s daným klíčem
Množinu všech možných klíčů, které se mohou ve slovníku vyskytnout, nazveme univerzum \(\mathcal{U}\).

Pro menší rozsahy univerza \(\mathcal{U}\) lze použít například bitové pole.
Potom časová složitost operací bude zjevně \(O(1)\).
Nicméně paměťové nároky budou \(\Theta(|\mathcal{U}|)\).
V praxi ale bývá velikost univerza \(|\mathcal{U}|\) obrovské číslo.
Podobně tabulka s přímým adresováním podle klíčů.
Klasické slovníky (překladové, výkladové) používají (abecedně) seřazená pole: hledání je logaritmické, vkládání či mazání je lineární.
V této kapitole se budeme věnovat hešovacím tabulkám (hash tables, alternativně se jim říká rozptylovací tabulky).
Cílem hešování je skloubit nízké paměťové nároky operací, tzn. \(O(|K|)\), a přitom zachovat konstantní složitost operací, i když pouze v průměrném případě.

Pro nějaké univerzum klíčů \(\mathcal{U}\), zvolme konečné pole přihrádek \(P = \{0,...,m − 1\}\) (hešovací tabulku) a hešovací funkci \(h: \mathcal{U} \to P\), která každému klíči univerza přidělí jednu přihrádku.
Chceme-li uložit množinu prvků s klíči \(K \subseteq \mathcal{U}\), rozmístíme její prvky do přihrádek: prvek s klíčem \(k \in K\) umístíme do přihrádky \(h(k)\).
Budeme-li hledat nějaký prvek s klíčem \(k \in \mathcal{U}\), víme, že nemůže být jinde než v přihrádce \(h(k)\).
Díky poměru \(m\) a \(|U|\ (m \ll |\mathcal{U}|)\) se bude stávat, že několik prvků padne do stejné přihrádky.
Tomu se říká kolize
Cílem je volit \(m\) a \(h\) tak, aby se počet kolizí minimalizoval.
To, jak kolize řešit, vysvětlíme později.

Uvažujme univerzum všech celých čísel, hešovací tabulku s \(m = 10\) přihrádkami a hešovací funkci \(h(k) = k mod 10\).
Celočíselné klíče budeme tedy rozdělovat do přihrádek podle poslední číslice.
Předpokládejme, že jsme do tabulky vložili letopočty 1212, 935, 1948, 1918, 1968, 1989

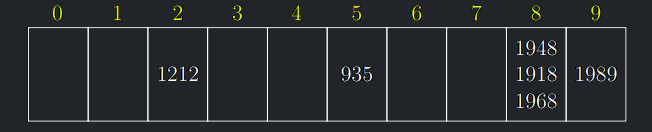
Image title

Hledáme-li rok 2015, víme, že se musí nacházet v přihrádce 5. Tam je ovšem pouze 935, takže hned odpovíme zamítavě.
Hledání roku 2017 je ještě rychlejší: přihrádka 7 je prázdná.
Hledáme-li rok 1618, musíme ho porovnat s 3 prvky.