6.5 AVL operace
AVLInsert
Idea
- Nový vrchol vložíme standardně jako list se znaménkem \(\mathbf{0}\)
- Z prázdného podstromu hloubky \(0\) se tak stal jednovrcholový podstrom hloubky \(1\)
- Potom je třeba přepočítat hloubky stromů na cestě z jeho rodiče do kořene.
- Proto budeme propagovat nahoru informaci o tom, že se zvětšila hloubka podstromu.
- V jednotlivých úrovních se tato informace zpracuje v závislosti na hloubkách příslušných sourozenců.
- Tuto kontrolu a případné napravení nevyvážeností můžeme elegantně provést během návratu z rekurze v proceduře AVLInsert
Oprava hloubkového vyvážení
Popíšeme propagaci pro jeden vrchol:
- Nechť do nějakého vrcholu \(x\) přišla z jeho syna informace o prohloubení podstromu.
-
Ukážeme pro případ, kdy přišla z levého syna
- Případ, kdy přišla z pravého syna, se řeší obdobně, jen se vymění význam \(\mathbf{+1}\) a \(\mathbf{-1}\), levého a pravého podstromu a směr rotací.
- Rozlišíme tři případy podle znaménka vrcholu \(x\)
Případ 1 - vrchol x měl znaménko +1
- Hloubka levého podstromu se právě vyrovnala s hloubkou pravého, čili znaménko \(x\) se změní na \(\mathbf{0}\)
- Hloubka podstromu \(T(x)\) se ale nezměnila, takže propagování informace zastavíme.
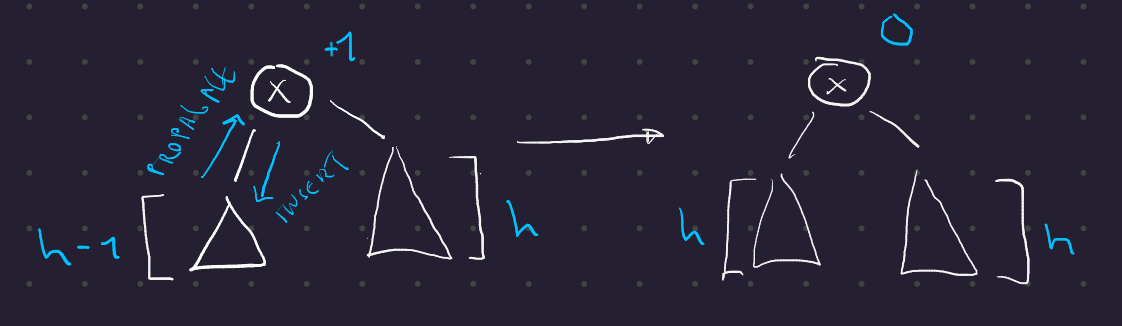
AVLInsert případ 1
Případ 2 - vrchol x měl znaménko 0
- Znaménko \(x\) se změní na \(\mathbf{-1}\).
- Hloubka podstromu \(T(x)\) se zvětšila o jedna, takže musíme pokračovat v propagování
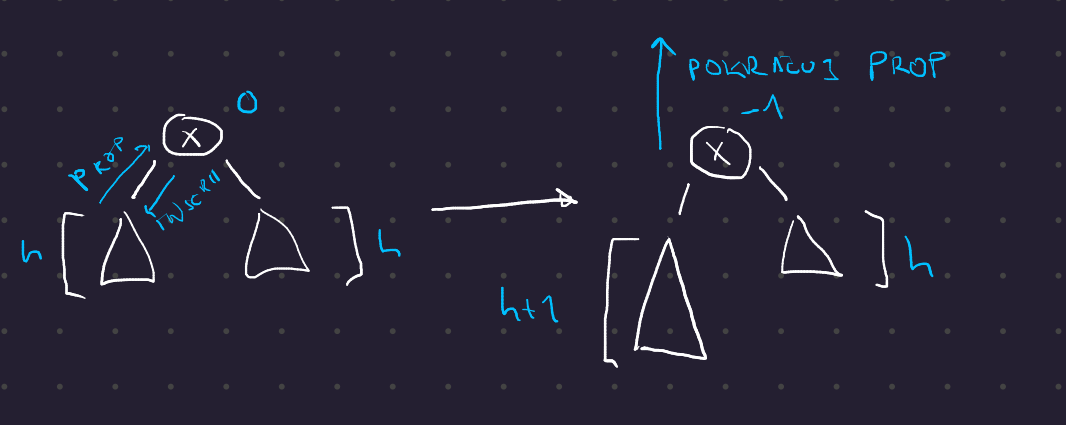
AVLInsert případ 2
Případ 3 - vrchol x měl znaménko -1
tedy teď získá \(\delta(x) = \mathbf{-2}\), je třeba vyvažovat
- Označme \(y\) vrchol, z nějž přišla informace o prohloubení, čili levého syna vrcholu \(x\)
- Rozebereme opět tři případy podle znaménka vrcholu \(y\)
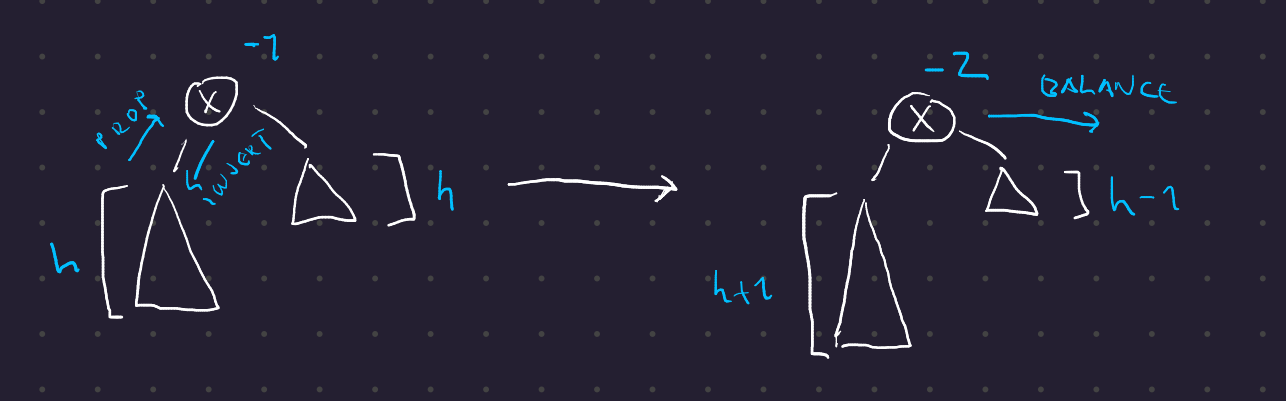
AVLInsert případ 3 (obecně)
Případ 3a - vrchol y má znaménko -1
- Označíme-li \(h\) hloubku podstromu \(C\), podstrom \(T(y)\) má hloubku \(h + 2\), takže podstrom \(A\) má hloubku \(h + 1\) a podstrom \(B\) hloubku \(h\).
- Provedeme jednoduchou rotaci \(R\) hrany \(\{x, y\}\)
- Tím získá vrchol \(x\) znaménko \(\mathbf{0}\), podstrom \(T(x)\) hloubku \(h + 1\), vrchol \(y\) znaménko \(\mathbf{0}\) a podstrom \(T(y)\) hloubku \(h + 2\)
- Jelikož před započetím operace AVLInsert měl podstrom \(T(x)\) hloubku \(h + 2\), z pohledu vyšších pater se nic nezměnilo. 5
- Propagování (červená šipka) tedy zastavíme
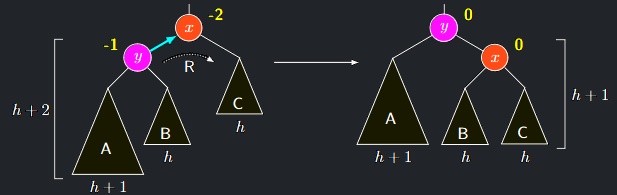
AVLInsert případ 3a
Případ 3b - vrchol y má znaménko +1
- Označíme \(z\) pravého syna vrcholu \(y\) (musí existovat).
- Označíme jednotlivé podstromy tak jako na obrázku a spočítáme jejich hloubky.
- Referenční hloubku \(h\) zvolíme podle podstromu \(D\)
- Hloubky \(h−\) znamenají buď \(h\) nebo \(h − 1\)
- Provedeme dvojitou LR rotaci, která celou konfiguraci překoření za vrchol \(z\)
- Vrchol \(x\) bude mít znaménko buď \(\mathbf{0}\) nebo \(\mathbf{+1}\), vrchol \(y\) buď \(\mathbf{-1}\) nebo \(\mathbf{0}\), každopádně oba podstromy \(T(x)\) a \(T(y)\) získají hloubku \(h + 1\)
- Proto vrchol \(z\) získá znaménko \(\mathbf{0}\)
- Před započetím AVLInsertu činila hloubka celé konfigurace \(h + 2\), nyní je také \(h + 2\), takže propagování zastavíme
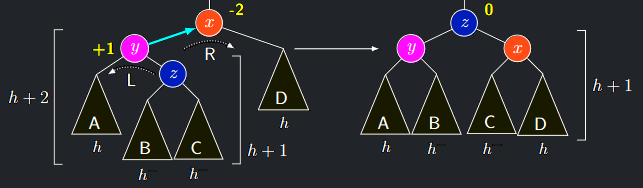
AVLInsert případ 3b
Případ 3c - vrchol y má znaménko 0
- Tento případ nemůže nikdy nastat, neboť z vrcholu se znaménkem \(\mathbf{0}\) se informace o prohloubení v žádném z předchozích případů nešíří a nově přidaný list má sice znaménko \(\mathbf{0}\), ale jeho otec nemůže mít nikdy \(\mathbf{-1}\)
- Čili zdola z vrcholu se znaménkem \(\mathbf{0}\) nemůže informace o prohloubení přijít do vrcholu se znaménkem \(\mathbf{-1}\)
AVLDelete
Idea
Obdobně jako AVLInsert.
- Vrchol smažeme podle BVSDelete a po cestě zpět do kořene propagujeme informaci o snížení hloubky podstromu.
- Pokaždé mažeme list nebo vrchol s jediným synem, takže stačí propagovat od místa smazaného vrcholu nahoru.
Oprava hloubkového vyvážení
Popíšeme propagaci pro jeden vrchol.
- Nechť do vrcholu \(x\) přišla ze syna informace o snížení hloubky podstromu.
-
Ukážeme opět pro případ, kdy přišla z levého syna.
- Případ, kdy přišla z pravého syna se řeší obdobně, jen se vymění význam \(\mathbf{+1}\) a \(\mathbf{-1}\), levého a pravého podstromu a směr rotací.
- Rozlišíme opět tři případy podle znaménka vrcholu \(x\).
Případ 1 - vrchol x má znaménko -1
- Hloubka levého podstromu se právě vyrovnala s hloubkou pravého, znaménko vrcholu \(x\) se mění na \(\mathbf{0}\)
- Hloubka podstromu \(T(x)\) se snížila, takže pokračujeme v propagování
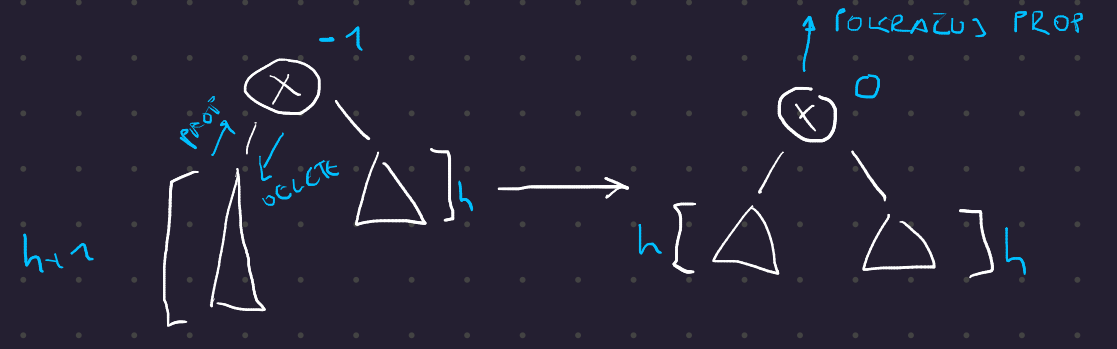
AVLDelete případ 1
Případ 2 - vrchol x má znaménko 0
- Znaménko \(x\) se změní na \(\mathbf{+1}\)
- Hloubka podstromu \(T(x)\) se nezměnila, takže propagování zastavíme
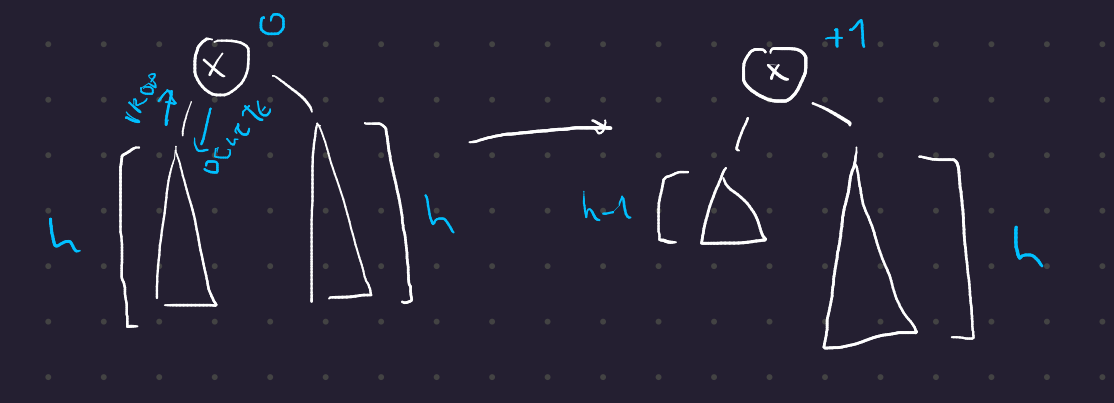
AVLDelete případ 2
Případ 3 - vrchol x má znaménko +1
- Tehdy se jeho znaménko změní na \(\mathbf{+2}\) a musíme vyvažovat.
- Rozlišíme tři případy podle znaménka pravého syna \(y\) vrcholu \(x\).
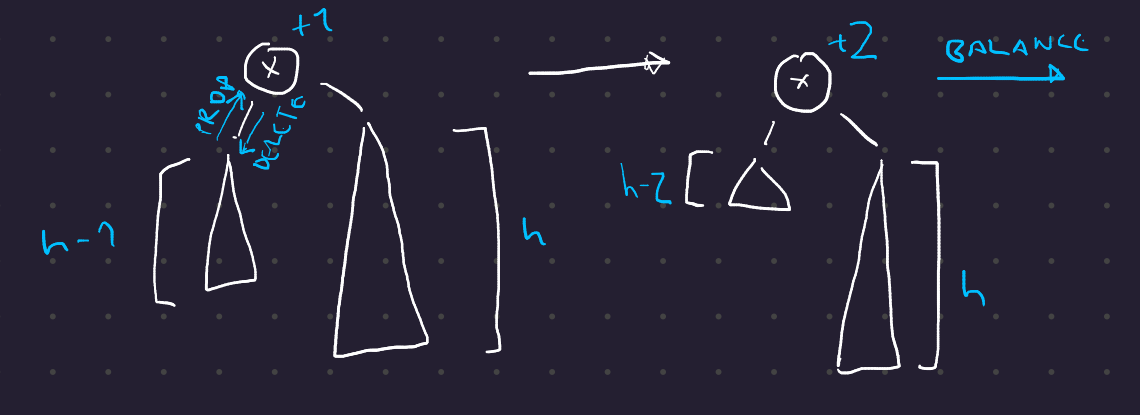
AVLDelete případ 3 (obecně)
Případ 3a - vrchol y má také znaménko +1
- Označíme-li \(h\) hloubku podstromu \(A\), bude mít \(T(y)\) hloubku \(h + 2\), takže \(C\) hloubku \(h + 1\) a \(B\) hloubku \(h\)
- Provedeme jednoduchou rotaci L hrany \(\{x, y\}\)
- Tím vrchol \(x\) získá znaménko \(\mathbf{0}\), podstrom \(T(x)\) hloubku \(h + 1\), takže vrchol y dostane také znaménko \(\mathbf{0}\)
- Před započetím AVLDelete měl podstrom \(T(x)\) hloubku \(h + 3\)
nyní má \(T(y)\) hloubku \(h + 2\), takže z pohledu vyšších hladin došlo ke snížení hloubky. - Proto pokračujeme v propagování (červená šipka).
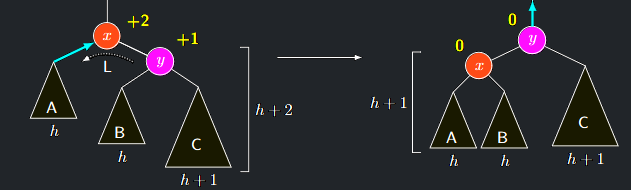
AVLDelete případ 3a
Případ 3b - vrchol y má znaménko 0
- Nechť \(h\) je hloubka podstromu \(A\). Pak \(T(y)\) má hloubku \(h + 2\) a \(B\) i \(C\) hloubku \(h + 1\).
- Provedeme jednoduchou rotaci L hrany \(\{x, y\}\)
- Vrchol \(x\) získává znaménko \(\mathbf{+1}\), podstrom \(T(x)\) hloubku \(h + 2\), takže vrchol \(y\) obdrží znaménko \(\mathbf{-1}\)
- Hloubka podstromu \(T(x)\) před začátkem AVLDelete činila \(h + 3\)$, nyní má podstrom \(T(y)\) hloubku také \(h + 3\), a propagování zastavíme
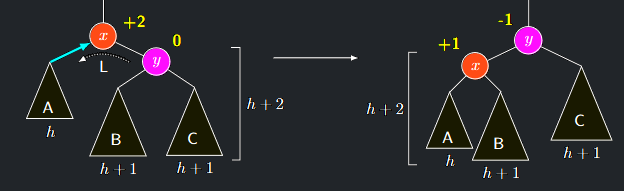
AVLDelete případ 3b
Případ 3c - vrchol y má znaménko -1
- Označíme \(z\) levého syna vrcholu \(y\)
- Označíme podstromy podle obrázku a spočítáme jejich hloubky.
- Referenční hloubku \(h\) zvolíme opět podle \(A\)
- Hloubky \(h−\) znamenají buď \(h\) nebo \(h − 1\)
- Provedeme dvojitou RL rotaci, která celou konfiguraci překoření za vrchol \(z\)
- Přepočítáme hloubky a znaménka.
- Vrchol \(y\) bude mít znaménko buď \(\mathbf{0}\) nebo \(\mathbf{+1}\), \(x\) buď \(\mathbf{-1}\) nebo \(\mathbf{0}\).
- Podstromy \(T(y)\) a \(T(x)\) budou každopádně hluboké \(h + 1\)
- Proto vrchol \(z\) obdrží znaménko \(\mathbf{0}\)
- Původní hloubka podstromu \(T(x)\) před začátkem AVLDelete činila \(h + 3\), nyní hloubka \(T (z)\) činí \(h + 2\)
- pokračujeme v propagování (červená šipka).
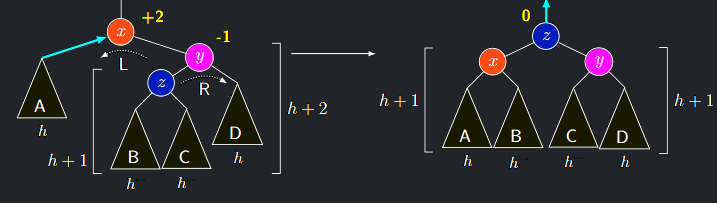
AVLDelete případ 3c
Věta 6.3 (o složitosti operací AVLInsert a AVLDelete)
Věta o složitosti operací AVLInsert a AVLDelete
AVLInsert a AVLDelete trvají \(O(log n)\)
Důkaz Věty 6.3
- Hloubka AVL stromu je vždy \(\Theta(log n)\)
- Původní implementace operací BVSFind, BVSInsert a BVSDelete tedy pracují v logaritmickém čase.
- Při vyvažování se operace vždy vrací po cestě do kořene a v každém vrcholu provede \(\Theta(1)\) operací, takže celkově také trvá \(\Theta(log n)\)