Hloubkové vyvážení: AVL stromy
- Z předchozího výkladu tedy plyne, že žádné kritérium vyváženosti stejně jako příliš přísné kritérium vyváženosti vedou v nejhorším případě na lineární složitost alespoň jedné z operací BVS.
- Kritérium vyváženosti BVS je tedy třeba definovat méně restriktivně, stačí udržovat hloubku \(O(logn)\).
Definice 6.3 (Hloubkově vyvážený BVS)
Hloubkově vyvážený BVS
BVS je hloubkově vyvážený, pokud pro každý jeho vrchol \(v\) platí
- Existuje několik různých řešení, zde si vysvětlíme tzv. AVL-stromy, které jsou efektivní implementací hloubkově vyvážených BVS.
Věta 6.2 (o hloubce hloubkově vyvážených stromů)
Věta o hloubce hloubkově vyvážených stromů
Hloubkově vyvážený strom s \(n\) vrcholy má hloubku \(\Theta (log n)\)
Důkaz Věty 6.2
- Definujme \(A_{h} =\) min. počet vrcholů HV stromu hloubky \(h\)
- Ukážeme, že \(A_{h}\) roste exponenciálně s \(h\)
- Nejmenší takové stromy dané hloubky jsou maximálně "hloubkově vyvážené" v mezích definice, čili v každém vnitřním
vrcholu v platí \(|h(L(v)) − h(R(v))| = 1.\)
Pro \(h \le 4\) lze nejmenší HV stromy hloubky \(h\) nalézt přímo:
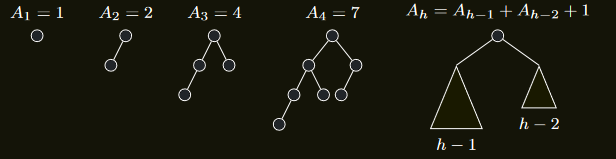
- Obecně pak minimální HV strom hloubky \(h\) musí mít jako podstromy minimální HV stromy hloubky \(h − 1\) a \(h − 2\)
- Musí tedy platit \(A_{h} = A_{h−1} + A_{h−2} + 1\)
-
Dokážeme indukcí, že \(A_{h+1} \geq 2^{\frac{h}{2}} \stackrel{\cdot}{=} 1.41^{h}\)
- IZ: \(A_{1} = 1 \geq 2^{\frac{0}{2}} = 1\) a \(A_{2} = 2 \geq 2^{\frac{1}{2}}\)
- IK:
\[ \begin{align} A_{h+1} & = 1 + A_{h} + A_{h-1} \gt \\\\ & \gt 2^{\frac{h-1}{2}} + 2^{\frac{h-2}{2}} = \\\\ & = 2^{\frac{h}{2}} \cdot (2^{-\frac{1}{2}} + 2^{-1}) \gt \\\\ & \gt 2^{\frac{h}{2}} \cdot (\frac{1}{2} + \frac{1}{2}) = \\\\ & = 2^{\frac{h}{2}} \end{align} \] -
HV strom hloubky \(h + 1\) má tedy nejméně \(\sqrt{2^{h}}\) vrcholů.
- Proto HV strom o \(n\) vrcholech má hloubku nejvýše \(log_{\sqrt{2}}(n) + 1\)
- A protože je binární, nemůže mít hloubku menší než \(⌊log_{2} n⌋\)
- Tedy hloubka HV stromu o \(n\) vrcholech je \(\Theta (log n)\)
Udržování hloubkového vyvážení
- Operace BVSShow, BVSMin, BVSPred a BVSFind nemění ani tvar ani obsah BVS, fungují tedy beze změny i pro AVL stromy.
- Operace vkládání a mazání prvků ale hloubky podstromů mění.
- Proto operace AVLInsert a AVLDelete vloží/vyjmou vrchol jako u BVSInsert a BVSDelete, ale pak kontrolují směrem ke kořenu hloubkovou vyváženost a při jejím porušení ji opravují
Jak kontrolovat a případně opravit hloubkovou nevyváženost?
- V každém vrcholu v vždy spočteme číslo \(\delta(v) = h(R(v)) − h(L(v))\), které nazveme znaménko vrcholu \(v\).
-
V korektním AVL stromu může nabývat jen těchto hodnot:
- \(\delta (v) = +1\) (pravý podstrom hlubší) – značíme \(+1\)
- \(\delta (v) = −1\) (levý podstrom hlubší) – značíme \(-1\)
- \(\delta (v) = 0\) (oba podstromy stejně hluboké) – značíme \(0\)
-
Jakmile při kontrole narazíme na jiné \(\delta(v)\), strom opravíme pomocí jednoduchých nebo dvojitých rotací
AVL rotace
Jednoduché AVL rotace
Jednoduchá rotace doprava (R)
- Jednoduchá rotace doprava opraví hloubkovou nevyváženost v modelové situaci dle obrázku dole, kdy:
- \(y = ℓ(x)\) a \(h = h(B) = h(C) = h(A) − 1\) a tudíž
- \(\delta (y) = \mathbf{-1}\) a \(\delta (x) = \mathbf{-2}\)
- Po provedení rotace doprava je \(\delta (x) = \delta(y) = 0\)
- Z definice BVS plyne, že přepojení \(B\) od \(y\) k \(x\) zachovává BVS
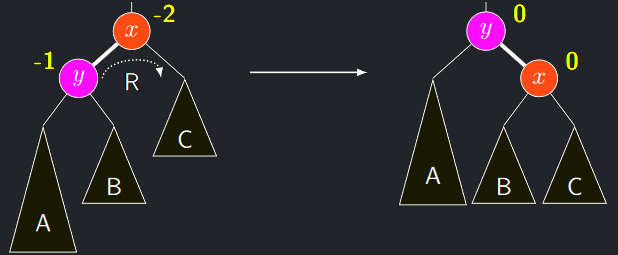
Jednoduchá rotace doprava v AVL stromu
Jednoduchá rotace doleva (L)
- Jednoduchá rotace doleva je zrcadlově symetrická modelová situace:
- \(y = r(x)\) a \(h(A) = h(B) = h(C) − 1\) a tudíž
- \(\delta(x) = \mathbf{+2}\) a \(\delta(y) = \mathbf{+1}\)
- Po provedení rotace doleva je opět \(\delta(x) = \delta(y) = 0\)
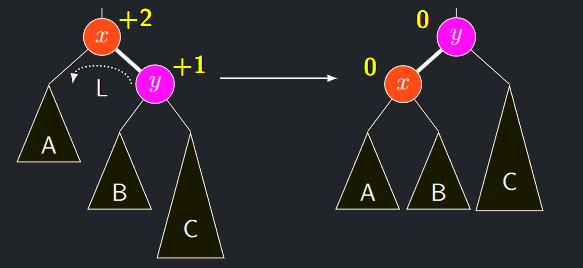
Jednoduchá rotace doleva v AVL stromu
Algoritmus 6.7 (rotateLeft)
Algoritmus rotateLeft
Vstup
- Vrchol \(x\) v BVS
- Vnější algoritmus poté musí případnou změnu hloubky podstromu propagovat sám.
Pozorování
Pokud je \(x\) vrcholem v binárním vyhledávacím stromě, potom po volání rotateLeft\((x)\) máme opět binární vyhledávací strom.
Pozorování
- Vše platí symetricky pro rotateRight\((x)\)
Dvojité AVL rotace
Situace, kdy jednoduchá rotace nepomůže
- Lze snadno nahlédnout, že jednoduchá rotace nepomůže v modelové situaci na obrázku, kdy \(h(A) = h(C) = h(B) − 1\)
- Ukázáno pro rotaci doprava: místo \(\delta(y) = \mathbf{+1}\) a \(\delta(x) = \mathbf{-2}\) dostaneme \(\delta(y) = \mathbf{+2}\) a \(\delta(x) = \mathbf{-1}\)
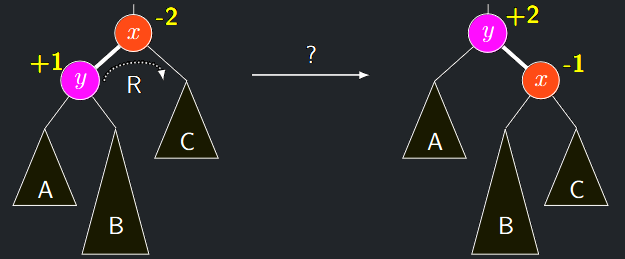
- V podobných situacích je nutné použít posloupnost dvou jednoduchých rotací, buď LR nebo RL, které nazýváme dvojité rotace.
Dvojitá rotace LR
- Nechť \(h(A) = h(B) = h(D) = h(C) + 1\)
- A tedy \(\delta(x) = \mathbf{-2}, \delta(y) = \mathbf{+1}\) a \(\delta(z) = \mathbf{-1}\)
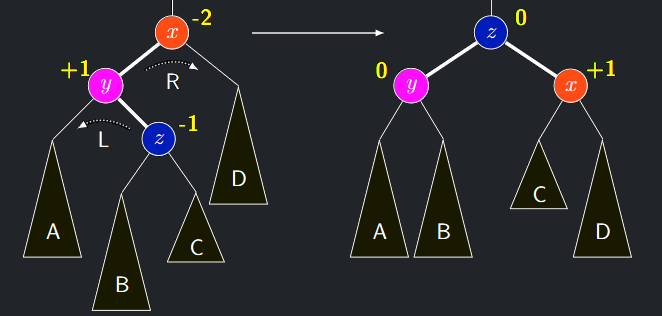
LR rotace
- Po provedení LR rotace máme \(\delta(y) = \delta(z) = \mathbf{0}\) a \(\delta(x) = \mathbf{+1}\)
- Funguje zjevně i pro situace, kde je na počátku \(\delta(z) = \mathbf{+1}\) nebo \(\delta(y) = \mathbf{+2}\)
Dvojitá rotace RL
- Nechť opět symetricky \(h(A) = h(B) = h(D) = h(C) + 1\)
- A tedy \(\delta(x) = \mathbf{+2}, \delta(y) = \mathbf{-1}\) a \(\delta(z) = \mathbf{-1}\)
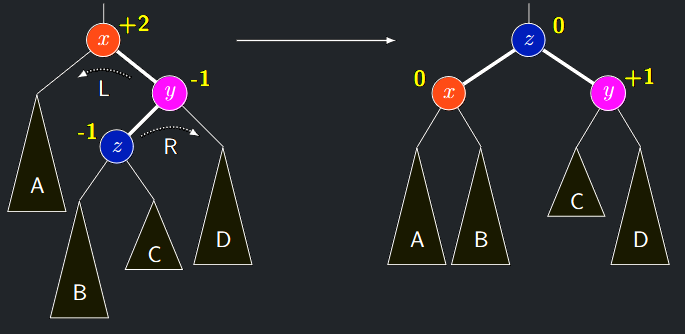
RL rotace
- Po provedení RL rotace máme \(\delta(x) = \delta(z) = \mathbf{0}\) a \(\delta(y) = \mathbf{+1}\)
- Funguje zjevně, i když je na počátku \(\delta(z) = \mathbf{+1}\) nebo \(\delta(y) = \mathbf{-2}\)