Skip to content

6.3 Vyváženost BVS

Pozorování

Časová složitost operací BVSFind, BVSMin, BVSInsert a BVSDelete nad BVS \(T(v)\) je:

\[ O(h(T (v))) \]

Pozorování

Hloubka \(h(T(v))\) BVS \(T(v)\) je:

  • v nejlepším případě \(\Omega(log |T (v)|)\)
  • v nejhorším případě \(O(|T (v)|)\) (např. BVS vytvořený postupným vložením klíčů \(1, 2, . . . , n\) v tomto pořadí).

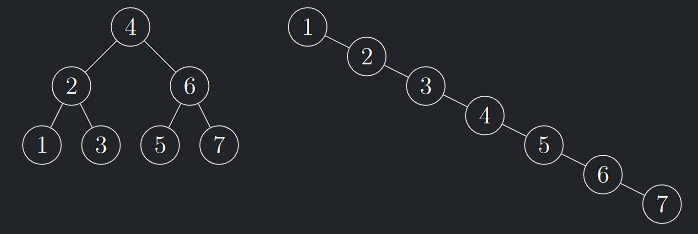
Image title

Dva BVS se stejnými vrcholy a jinou hloubkou

Definice 6.2 (Dokonale vyvážený BVS)

Dokonale vyvážený BVS

BVS nazveme dokonale vyvážený, pokud pro každý jeho vrchol \(v\) platí

\[ ||L(v)| − |R(v)|| ≤ 1 \]

Pozorování

Dokonale vyvážený BVS o velikosti \(n\) má \(1 + ⌊log n⌋\) hladin a operace BVSFind, BVSMin, BVSInsert a BVSDelete na něm tedy mají časovou složitost \(O(logn)\)

Věta 6.1 (o složitosti operací nad dokonale vyváženým BVS)

Věta o složitosti operací nad dokonale vyváženým BVS

Pokud má BVS zůstávat po provedení operací BVSInsert a BVSDelete dokonale vyvážený, potom ať použijeme jakoukoli implementaci zmíněných operací, bude časová složitost aspoň jedné z nich \(\Omega (n)\) pro nekonečně mnoho různých \(n\)

Důkaz Věty 6.1

Uvažujme dokonale vyvážený BVS s klíči \(1, 2, . . . , n\), kde \(n = 2^{k} - 1\)
Ten pak vypadá nutně takto:

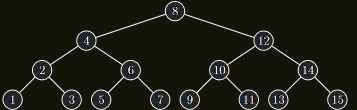
Image title

  1. Kořen stromu je vždy prostřední z klíčů.
  2. Všechna lichá čísla jsou v listech stromu.
  3. Levý a pravý podstrom mají právě \(2^{k−1} − 1\) vrcholů a jsou tedy opět určeny jednoznačně.
  4. Nyní provedeme následující posloupnost dvojic operací:
    \(Insert(n + 1), Delete(1), Insert(n + 2), Delete(2), . . .\)
  5. Po provedení i-té dvojice operací bude strom obsahovat hodnoty \(i + 1, . . . , i + n\)
  6. Podle toho, zda je \(i\) sudé nebo liché, se budou v listech nacházet buď všechna sudá, nebo všechna lichá čísla.
  7. Pokaždé se proto všem vrcholům změní, zda jsou listy, což ale nutně znamená upravit \(\Omega (n)\) ukazatelů.
  8. Tedy aspoň jedna z operací BVSInsert a BVSDelete trvá \(\Omega (n)\)