Přehled operací BVS
| Operace | Komplexita | Popis |
|---|---|---|
| BVSShow\((v)\) | \(O(n)\) | Vypiš vzestupně uspořádanou posloupnost klíčů všech vrcholů \(T (v).\) |
| BVSMin\((v)\) | \(O(logn)\) | Vrať vrchol obsahující minimální klíč v \(T (v)\) |
| BVSMax\((v)\) | \(O(logn)\) | Vrať vrchol obsahující maximální klíč v \(T (v)\) |
| BVSPred\((v,w)\) | \(O(logn), \Theta^{*}(1)\) | Vrať předchůdce vrcholu \(w\) v \(T(v)\) |
| BVSSucc\((v,w)\) | \(O(logn), \Theta^{*}(1)\) | Vrať následníka vrcholu \(w\) v \(T(v)\) |
| BVSFind\((v, x)\) | \(O(logn)\) | Vrať vrchol v \(T(v)\) s klíčem \(x\), pokud takový existuje |
| BVSInsert\((v,x)\) | \(O(logn)\) | Vlož do \(T(v)\) nový vrchol s klíčem \(x\), pokud v něm ještě neexistuje |
| BVSDelete\((v,x)\) | \(O(logn)\) | Odstraň z \(T(v)\) vrchol s klíčem \(x\), pokud takový existuje |
Komplexita operací v této tabulce uvažuje hloubkově vyvažovaný strom, pro nevyvažovaný strom by byla komplexita všech operací \(O(n)\)
Operace BVS
BVSShow
Algoritmus 6.1 (BVSShow)
Algoritmus BVSShow
Vstup
Ukazatel na kořen \(v\) nějakého BVS \(T(v)\)
Výstup
Vzestupně uspořádaná posloupnost klíčů všech vrcholů v \(T(v)\)
Pozorování
BVSShow\((v)\) vypíše vzestupně uspořádané klíče vrcholů BVS \(T(v)\) v čase \(O(|T(v)|)\)
BVSMin
- Nalezení vrcholu s maximálním klíčem je analogické.
Pozorování
Nejmenší klíč je první v posloupnosti vzestupně uspořádaných klíčů vygenerovaných v předchozím algoritmu InOrder průchodem a tudíž vrchol s nejmenším klíčem je v daném BVS ten nejvíce vlevo. Je to tudíž buď list nebo vrchol s jedním synem.
Algoritmus 6.2 (BVSMin)
Algoritmus BVSMin
Vstup
Ukazatel na kořen \(v\) nějakého BVS \(T(v)\)
Výstup
Ukazatel na vrchol obsahující nejmenší klíč v \(T(v)\)
BVSPred
Pozorování
- Klíč předchůdce prvku \(w\) v \(T(v)\) je ve vzestupném výpisu klíčů algoritmem BVSShow levým sousedem \(k(w).\)
- Pokud má \(w\) v \(T(v)\) levý podstrom \(L(w)\), pak je předchůdce w jeho maximem.
- V opačném případě je předchůdcem \(w\) první předek, do kterého vstoupíme zprava při průchodu nahoru.
- Evidentně, prvek s nejmenším klíčem předchůdce nemá, neboť nesplňuje ani jednu podmínku
Algoritmus 6.3 (BVSPred)
Algoritmus BVSPred
Vstup
Ukazatel na kořen \(v\) nějakého BVS \(T(v)\) a na nějaký jeho vrchol \(w\)
Výstup
Ukazatel na předchůdce \(w\) v \(T(v)\)
K zamyšlení
Ověřte, že pro \(w =\) BVSMin(\(v\)) vrací tento algoritmus \(\emptyset\)
BVSFind
- Hledání vrcholu BVS s daným klíčem
Algoritmus 6.4 (BVSFind)
Algoritmus BVSFind
Vstup
Ukazatel na kořen \(v\) nějakého BVS \(T(v)\) a klíč \(x\)
Výstup
Ukazatel na vrchol s klíčem \(x\), pokud takový v \(T(v)\) existuje, jinak \(\emptyset\)
Pozorování
Korektnost plyne okamžitě z definice BVS:
- V libovolném vrcholu \(u\) platí, že všechny klíče v \(L(u)\) jsou menší než \(k(u)\)
- Všechny klíče v \(R(u)\) jsou větší než \(k(u)\)
BVSInsert
- Vložení vrcholu s daným klíčem do BVS
Algoritmus 6.5 (BVSInsert)
Algoritmus BVSInsert
Vstup
Ukazatel na kořen \(v\) nějakého BVS \(T(v)\) a klíč \(x\)
Výstup
Ukazatel na kořen \(v\) BVS s prvkem s klíčem \(x\)
Algoritmus
Pozorování
Operaci BVSInsert lze chápat jako hledání daného klíče a pokud klíč nenajdeme, vložíme ho na jednoznačně určenou pozici jako nový list (předpokládáme unikátní klíče)
Pozorování (tvar BVS)
- Z dosud uvedeného vyplývá, že danou množinu klíčů bude existovat více korektních BVS lišících se tvarem, protože výsledný tvar BVS závisí nejen na hodnotách klíčů, ale i na pořadí, v jakém jsou do BVS vkládány.
- Operace BVSShow vrátí pro všechny možné BVS nad stejnou množinou klíčů stejnou uspořádanou posloupnost klíčů.
- Geometricky tomuto lineárnímu výpisu odpovídá průmět na vodorovnou osu.
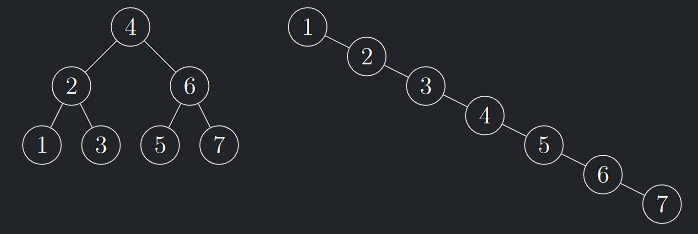
Tvar BVS
BVSDelete
- Odstranění vrcholu s daným klíčem z BVS
- Nejdříve nalezneme vrchol, který obsahuje klíč, který chceme smazat.
- Při mazání vrcholu může nastat několik různých případů:
Případy BVSDelete
1. Vrchol \(v\) není v \(T\)
- \(T\) je ponechán beze změny
2. Vrchol \(v\) je listem \(T\)
- Vrchol \(v\) je odstraněn z \(T\)
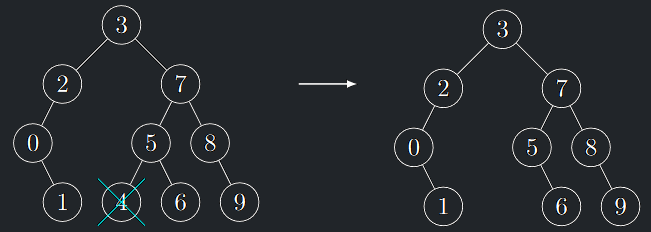
Odstranění listu BVS
3. Vrchol \(v\) má jednoho syna
- Vrchol \(v\) nahradíme jeho jediným synem
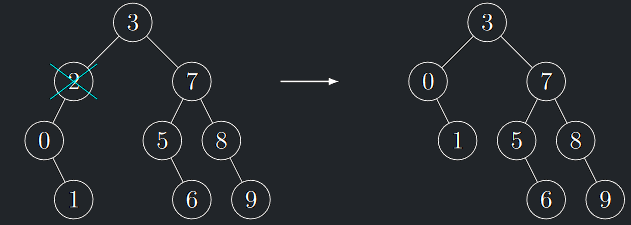
Odstranění vrcholu s jedním synem
4. Vrchol \(u\) má dva syny
- Pak \(u\) nemůžeme odstranit přímo, protože by nebylo kam připojit jeho syny.
- Využijeme ale faktu, že vrchol \(u\) má v BVS následníka \(w\) = BVSMin(r(u)).
- A ten má nejvýše jednoho syna (pravého, kdyby měl levého, tak je následník jeho levý syn)
- Klíč vrcholu \(u\) nahradíme klíčem vrcholu \(w\)
- Aplikací postupu z případu 2) nebo 3) pak odstraníme z BVS vrchol \(w\).
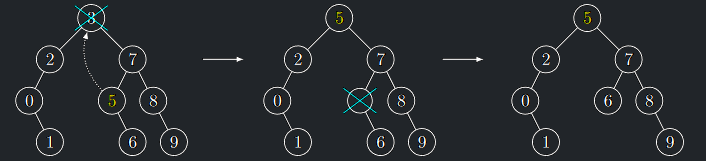
Odstranění vrcholu se dvěma syny
Algoritmus 6.6 (BVSDelete)
Algoritmus BVSDelete
Vstup
Ukazatel na kořen \(v\) nějakého BVS a klíč \(x\)
Výstup
Ukazatel na kořen BVS, ze kterého byl odstraněn vrchol s klíčem \(x\), pokud takový vrchol existoval.
Algoritmus