6.1 Úvod do BVS
Binární strom (opakování)
Strom nazveme binární, pokud
- je zakořeněný
- každý vrchol má nejvýše dva syny
- u synů rozlišujeme, který je levý a který pravý.
Značení
Pro vrchol v binárního stromu \(T\) značíme
- \(ℓ(v)\) a \(r(v)\): levý a pravý syn vrcholu \(v\)
- \(L(v)\) a \(R(v)\): levý a pravý podstrom vrcholu \(v\)
- \(p(v)\): otec vrcholu \(v\)
- \(T(v)\): podstrom tvořený kořenem v a všechny jeho potomky
- \(h(T(v))\): hloubka stromu \(T(v)\) je počet hladin \(T(v)\)
- \(|T|, |T (v)|, |L(v)|, |R(v)|\): počet vrcholů stromu \(T , T(v), L(v)\) a \(R(v)\)
- Pokud vrchol v nemá levého syna, položíme \(ℓ(v) = \emptyset.\)
- Podobně pro \(r(v)\) a \(p(v)\)
- Pak dodefinujeme, že \(T (\emptyset)\) je prázdný strom a \(h(T (\emptyset)) = 0.\)
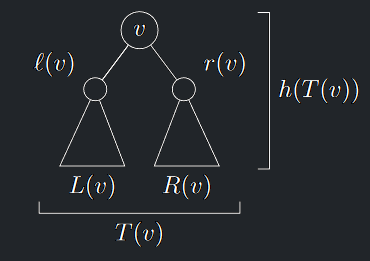
Značení binárního stromu
Konvence zápisu pseudokódu
- Binární strom budeme v paměti počítače reprezentovat pomocí spojových struktur.
- V algoritmech popisujících v pseudokódu operace nad binárními stromy budeme pracovat s ukazateli na jejich vrcholy.
Definice 6.1 (Binární vyhledávací strom)
Binární vyhledávací strom (BVS)
Binární vyhledávací strom (BVS) je binární strom, v jehož každém vrcholu \(v\) je uložen unikátní klíč \(k(v)\) a pro jehož každý vrchol \(v\) platí:
- Pokud \(a \in L(v)\), pak \(k(a) \lt k(v).\)
- Pokud \(b \in R(v)\), pak \(k(b) \gt k(v).\)
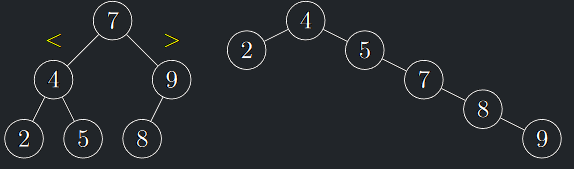
Příklady BVS