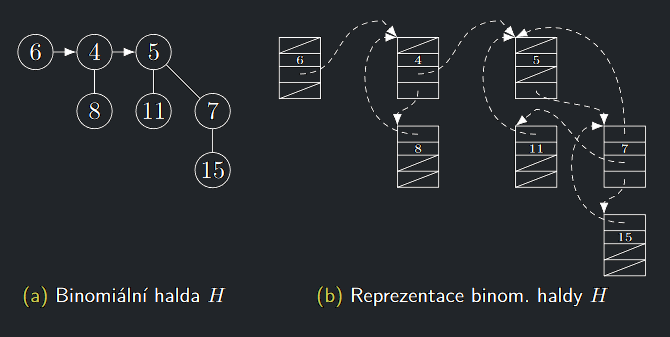
5.4 Reprezentace
Paměťová reprezentace prvků BH
Prvek v BH bude v počítači reprezentován pomocí následující struktury:
- Ukazatel na otce
- Ukazatel na levého sourozence
- Ukazatel na nejpravějšího syna
- Hodnota \(k(v)\)
Tvrzení
BHMergeTree i vytvoření BH ze seznamu synů kořene lze v čase \(O(log n)\), kde \(n\) je počet prvků ve výsledné BH
K Zamyšlení
Jak v minimové BH udělat operace:
- BHDecreaseKey v čase \(O(log n)\)?
- BHDelete v čase \(O(log n)\)?
- BHIncreaseKey v čase \(O(log n)\)?
Všechny operace dostanou ukazatel na prvek, se kterým se pracuje
Srovnání binární a binomiální haldy
| Operace | Binární | Binomiální |
|---|---|---|
| Vložení prvku do haldy velikosti \(n\) | \(O^{*}(log n), O(log n)\) | \(O^{*}(1), O(log n)\) |
| ExtractMin z haldy velikosti \(n\) | \(O(log n)\) | \(O(log n)\) |
| Sloučení 2 hald velikosti \(n\) | \(O(n)\) | \(O(log n)\) |
Binomiální haldy jsou nejjednodušším řešením tzv. mergeable heaps, které dokážou velmi efektivně provést operaci sloučení a ostatní operace mají na operaci sloučení postavené.