5.3 Operace na BH

Nalezení minima – BHFindMin(H):

Minimum celé BH se musí nacházet v jednom z kořenů stromů \(T_{i}\).
Stačí projít seznam \(\mathcal{T}\) , což bude trvat čas \(O(log n)\).
Používáme-li tuto funkci často, vyplatí se udržovat ukazatel na tento globálně nejmenší kořen. Operaci BHFindMin lze pak provést v konstantním čase.

Sloučení dvou BH – BHMerge

Sloučení dvou BH popíšeme nejdříve, protože se pomocí něho realizují ostatní operace.
Operace BHMerge ze dvou BH vytvoří jedinou, obsahující sjednocení prvků obou vstupních BH.
Nejprve popíšeme operaci BHMergeTree, která slije dohromady dva binomiální stromy stejného řádu \(B_{i}\) a vytvoří strom \(B_{i+1}\) (na to lze nahlížet i jako na sloučení dvou BH tvořených jediným binomiálním stromem stejného řádu).

Algoritmus 5.1 (BHMergeTree)

Algoritmus BHMergeTree

Vstup

Binomiální stromy \(T_{1}, T_{2}\) takové, že řád(\(T_{1}\)) = řád(\(T_{2}\))

Výstup

Výsledný strom \(T_{out}\)

Algoritmus

Pokud k(kořen(T1)) ≤ k(kořen(T2)):
    Připoj kořen(T2) jako nejpravějšího syna pod kořen(T1).
    Tout := T1
Jinak:
    Připoj kořen(T1) jako nejpravějšího syna pod kořen(T2).
Tout := T2

Pozorování

Algoritmus BHMergeTree\((T_{1}, T_{2})\), kde řád(\(T_{1}\)) \(=\) řád(\(T_{2}\)), vytvoří korektní binomiální strom s řádem řád(\(T_{1}\)) \(+ 1\)

Tvrzení

BH lze implementovat tak, že BHMergeTree\((T_{1}, T_{2})\) má časovou složitost \(O(1).\)

Image title

Idea algoritmu BHMerge pro sloučení dvou BH

Mějme BH \(A\) a \(B\), kde počet prvků \(A\) je \(a\) a v binárním zápise \(a = a_{k}a_{k−1} . . . a_{0}\) a počet prvků \(B\) je \(b = b_{ℓ}b_{ℓ−1} . . . b_{0}.\)
Výsledná halda \(C\) bude mít \(c = a + b\) prvků, \(c = c_{m}c_{m−1} . . . c_{0}.\)
Řády binomiálních stromů ve všech tří haldách jsou jednoznačně určeny binárním zápisem jejich počtu prvků.
Připomeňme "školní" algoritmus na sčítání binárních čísel \(a\) a \(b\) pod sebou:
jdeme od nejnižších řádů binárního zápisu k nejvyšším a
- výsledný bit \(c_{i} = (a_{i} + b_{i} +\) carry\(_{i})\) mod \(2\), kde carry\(_{i}\) je tzv. přenos z předchozího řádu a
- následně carry\(_{i+1}\) := \((a_{i} + b_{i} +\) carry\(_{i}\)) div \(2.\)

Binární sčítání - příklad

\(c_{i} = (a_{i} + b_{i} +\) carry\(_{i}\)) mod \(2\)
carry\(_{i+1}\) := \((a_{i} + b_{i} +\) carry\(_{i})\) div \(2\)

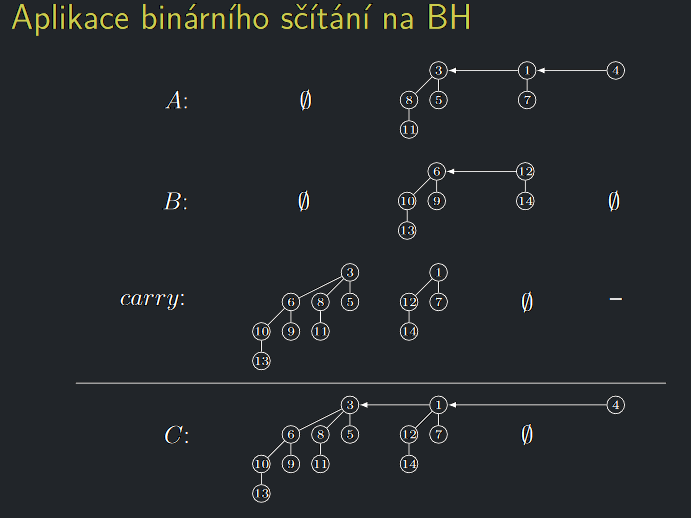
Image title

Aplikace binárního sčítání na BH

Algoritmus na vytvoření BH \(C\) nyní zrcadlí předchozí algoritmus sčítání binárních čísel s tím rozdílem, že:

Bity \(a_{i}, b_{i},\) carry\(_{i}\) budou nyní binomiální stromy \(A_{i}\), \(B_{i}\), carry\(_{i}\) řádu \(i\) nebo prázdné.
Místo sčítání dvou jedničkových bitů voláme BHMergeTree na dva binomiální stromy stejného řádu, což vytvoří strom vyššího řádu a tedy přenos carry do dalšího řádu.
Jsou-li všechny tři stromy \(A_{i}, B_{i},\) carry\(_{i}\) neprázdné, sloučíme \(A_{i}\) a \(B_{i}\) a výsledek se stane přenosem do vyššího řádu carry\(_{i+1}\) a do \(C_{i}\) přiřadíme carry\(_{i}\).
Protože udržujeme seznamy binomiálních stromů BH uspořádané dle jejich řádů, lze algoritmus realizovat průchodem dvou ukazatelů po těchto seznamech a přeskakováním řádů stromů nepřítomných v BH.

Image title

Algoritmus 5.2 (BHMerge)

Algoritmus BHMerge

BHMerge(A, B)

scitanci[0 . . . 2]         //pole aktuálních sčítanců
carry := null               //přenos
neprazdnych := 2            //počet zbývajících sčítanců
akt_rad := 0                //aktuální řád
Dokud neprazdnych ≥ 2:
    neprazdnych := 0
    pocet := 0              //počet sčítanců v aktuálním řádu
    Pokud A je neprázdná:
        neprazdnych++
        a := strom nejnižšího řádu v A
        Pokud řád(a) = akt_rad:
            scitanci[pocet]:= a
            pocet++
            vyřaď a z A
    Pokud B je neprázdná:
        neprazdnych++
        b := strom nejnižšího řádu v B
        Pokud řád(b) = akt_rad:
            scitanci[pocet]:= b
            pocet++
            vyřaď b z B
    Pokud carry není null:
        neprazdnych++
        scitanci[pocet]:= carry
        pocet++
        carry:= null

    Pokud pocet= 3:
        zapiš scitanci[2] do výstupu C
        carry := BHMergeTree(scitanci[0], scitanci[1])
    Pokud pocet= 2:
        carry := BHMergeTree(scitanci[0], scitanci[1])
    Pokud pocet= 1:
        zapiš scitanci[0] do výstupu C
    akt_rad++
Přeřaď do C zbytek BH A nebo B (pokud ještě něco zbývá)
Přepoj ukazatel na minimum na menší z minim z A a B

Věta 5.5 (o korektnosti a složitosti algoritmu BHMerge)

Věta o korektnosti a složitosti BHMerge

Algoritmus BHMerge je korektní a jeho časová složitost je \(O(log n).\)

Důkaz Věty 5.5

V každé iteraci se zpracují všechny stromy řádu akt_rad.
Následně se akt_rad zvýší o jedna.
Všechny operace uvnitř cyklu trvají čas \(O(1)\).
Nejvyšší řád je \(O(log n)\), celkový čas je tedy \(O(log n)\).

Vkládání prvku do BH - BHInsert

Algoritmus 5.3 (BHInsert)

Algoritmus BHInsert

BHInsert(H,x):
1 2	`Vytvoříme BH H′ s jediným prvkem x. BHMerge(H, H′)`

Image title

Věta 5.6 (o složitosti algoritmu BHInsert)

Věta o složitosti algoritmu BHInsert

Operace BHInsert má v nejhorším případě složitost \(O(log n).\) Pro na počátku prázdnou BH trvá posloupnost \(n\) volání operace BHInsert čas \(O(n).\) BHInsert má tedy amortizovanou časovou složitost \(O^{*}(1).\)

Důkaz Věty 5.6

Víme, že binomiální stromy tvořící \(n\)-prvkovou BH přesně odpovídají jedničkovým bitům v dvojkovém zápisu čísla \(n\).
Operace BHInsert je sloučení s jednoprvkovou BH a to odpovídá operaci Inc binární sčítačky.
Provedení operace BHMergeTree s \(O(1)\) složitostí během BHInsert odpovídá bitové inverzi v operaci Inc.
Dle analýzy binární sčítačky má tedy operace BHInsert amortizovanou složitost \(O^{*}(1)\).

Vytvoření n prvkové BH – BHBuild

Voláním BHInsert \(n\) krát po sobě vytvoříme BH o velikosti \(n.\)
Podle předchozí analýzy bude trvat vytvoření \(n\)-prvkové BH čas \(O(n).\)

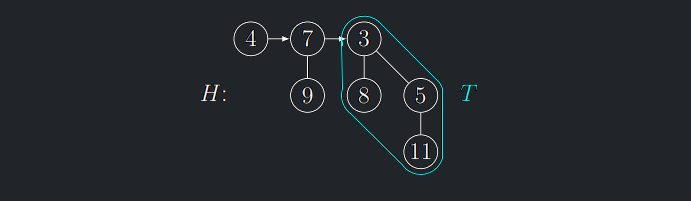
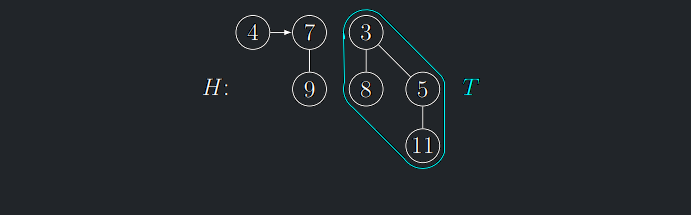
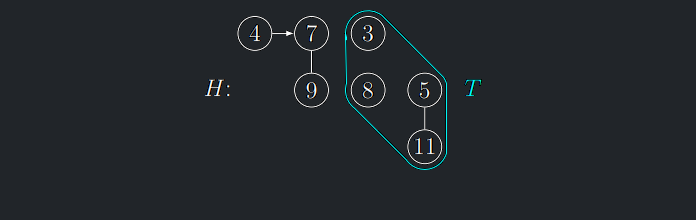
Odstranění minima z BH – BHExtractMin

Algoritmus 5.4 (BHExtractMin)

Algoritmus BHInsert

Najdi v BH H strom T , jehož kořen je minimem.
Odpoj tento strom T z BH H.
Odtrhni z T jeho kořen.
Z T vytvoř novou BH H′. -> POZOR
Proveď BHMerge(H, H′).

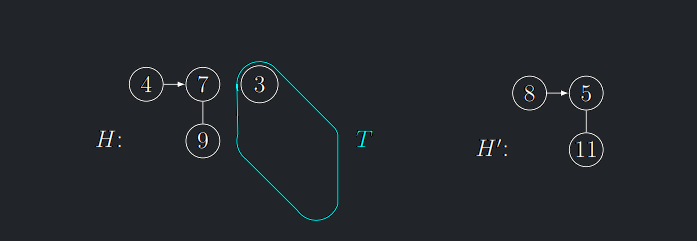
(4) Z T vytvoř novou BH H′

Potřebujeme v čase \(O(log n)\) vytvořit BH ze synů (podstromů) stromu \(\mathcal{T}\) .
Toho potřebujeme dosáhnout při zachování \(O(1)\) času pro BHMergeTree

Image title

Věta 5.7 (o složitosti algoritmu BHExtractMin)

Věta o složitosti algoritmu BHExtractMin

Časová složitost operace BHExtractMin je \(O(log n)\).

Důkaz Věty 5.7

Kroky \((1)\) a \((2)\) trvají čas \(O(1)\), stačí si udržovat minimový ukazatel na strom a vypojit ho ze seznamu.
Kroky \((3)\) a \((4)\) trvají \(O(logn)\), protože kořen binomiálního stromu má nejvýše \(O(logn)\) synů.
Sloučení hald trvá \(O(logn)\), včetně rekonstrukce minimového ukazatele.