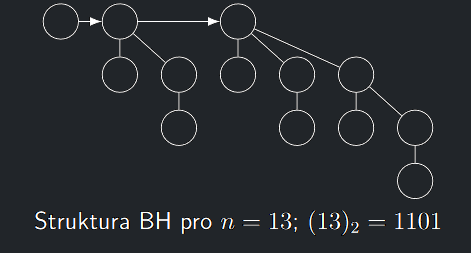
5.2 Binomiální halda
Definice 5.3 (Binomiální halda)
Binomiální halda
Binomiální halda (BH) obsahující \(n\) prvků je uspořádaná množina binomiálních stromů \(T = T_{1}, . . . , T_{ℓ}\), kde platí:
- Stromy \(T_{i}\) jsou v \(T\) uspořádány vzestupně podle svých řádů.
- \(n = |V (T_{1})| + · · · + |V (T_{ℓ})|.\)
- Pro každé nezáporné \(k\) se v množině \(T\) vyskytuje nejvýše jeden binomiální strom řádu \(k\).
- Každý vrchol \(v\) v každém stromu obsahuje klíč \(k(v)\).
- Pro každý strom \(T_{i}\) platí haldové uspořádání klíčů, čili
- \(\forall v \in V (T_{i})\) a pro všechny jeho syny \(s_{j} , j = 1, 2, . . . , m,\) platí \(k(v) \leq k(s_{j}).\)
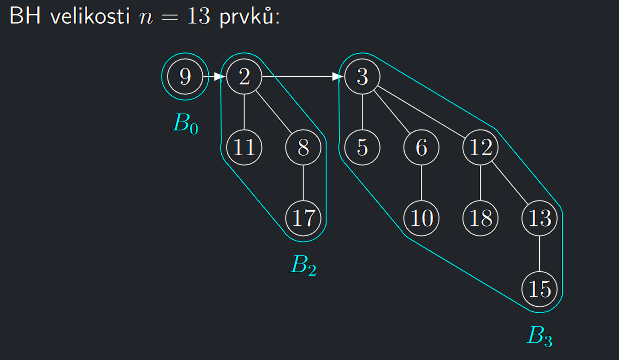
Paměťová reprezentace binomiální haldy v počítači
- Pro uložení uspořádané množiny stromů \(\mathcal{T}\) BH se používá spojový seznam.
- Seznamy synů jednotlivých vrcholů v binomiálních stromech budeme také udržovat ve spojových seznamech.
- Konkrétní implementaci prvku BH si předvedeme později, až budeme znát požadavky na operace, které s BH budeme provádět.
- Klíč prvku v budeme v pseudokódu značit \(k(v)\).
Vlastnosti binomiální haldy
Věta 5.4 (o existenci stromu \(B_{i}\) v BH)
Věta o existenci binomiálního stromu Bi v binomiální haldě
Binomiální strom \(B_{i}\) se vyskytuje v seznamu \(\mathcal{T}\) \(n\)-prvkové BH právě tehdy, když ve dvojkovém zápisu \(b_{k}b_{k−1} . . . b_{0}\) čísla \(n\) je \(b_{i} = 1\).
Důkaz Věty 5.4
Protože v BH nelze použít dva binomiální stromy stejného řádu a každý binomiální strom \(B_{i}\) přispěje do \(n\)-prvkové BH právě svými \(|V(B_{i})| = 2^{i}\) vrcholy, je poskládání \(n\) prvkové BH z binomiálních stromů ekvivalentní zápisu čísla \(n\) ve standardní dvojkové soustavě.
Důsledek
n-prvková BH má až \(O(log n)\) binomiálních stromů.