5.1 Binomiální stromy

Pro přehlednost zkracujeme jako BH. Podporuje stejné operace jako binární halda.
Navíc je schopna rychle provádět operaci sloučení dvou hald, která má u binární haldy lineární složitost (sloučit dvě binární haldy velikostí \(m\) a \(n\) má složitost operace HeapBuild haldy velikosti \(m + n\)).
Binomiální halda patří do rodiny tzv. mergeable heaps.
Další dobrou vlastností je vynikající amortizovaná složitost operace vkládání.
Nevýhodou jsou násobně vyšší paměťové nároky než u binární haldy.

Operace	Komplexita	Popis
BHInsert	\(O(log n), \Theta^{*}(1)\)	Vloží do BH nový prvek.
BHFindMin	\(O(1)\)	Vrátí minimum množiny prvků BH
BHExtractMin	\(O(log n)\)	Odstraní z BH minimum množiny jejích prvků
BHMerge	\(O(log n)\)	Sloučí dvě BH do jedné
BHBuild	\(O(n)\)	Postaví z \(n\) prvků BH
BHDecreaseKey	\(O(log n)\)	Sníží hodnotu klíče prvku BH.
BHIncreaseKey	\(O(log n)\)	Zvýší hodnotu klíče prvku BH.
BHDelete	\(O(log n)\)	Smaže prvek BH.

Definice 5.1 (Binomiální strom)

Binomiální strom řádu \(k\) (značíme \(B_{k}\)) je uspořádaný (t.j. záleží na pořadí synů) zakořeněný strom, pro který platí:

\(B_{0}\) je tvořen pouze kořenem.
Pro \(k \geq 1\) získáme \(B_{k}\) ze stromů \(B_{0}, B_{1}, . . . , B_{k−1}\) tak, že přidáme nový kořen a kořeny těchto stromů uděláme (takto popořadě) syny nového kořene

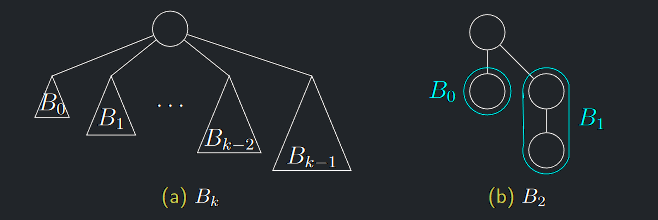
Image title

Definice 5.2 (Binomiální strom alternativně)

Binomiální strom řádu \(k\) (značíme \(B^{′}_{k}\)) je uspořádaný zakořeněný strom, pro který platí:

\(B^{′}_{0}\) je tvořen pouze kořenem.
Pro \(k \geq 1\) se \(B^{′}_{k}\) skládá ze stromu \(B^{′}_{k−1}\), pod jehož kořenem je jako nejpravější syn napojený další strom \(B^{′}_{k−1}\).

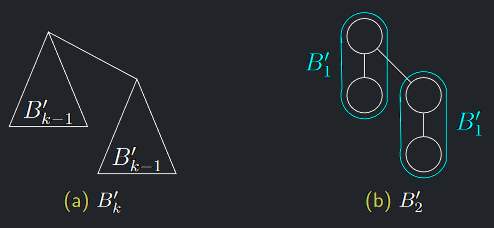
Image title

Věta 5.1 (o izomorfismu \(B_{k}\) a \(B^{′}_{k})\)

Stromy \(B_{k}\) a \(B^{′}_{k}\) jsou izomorfní

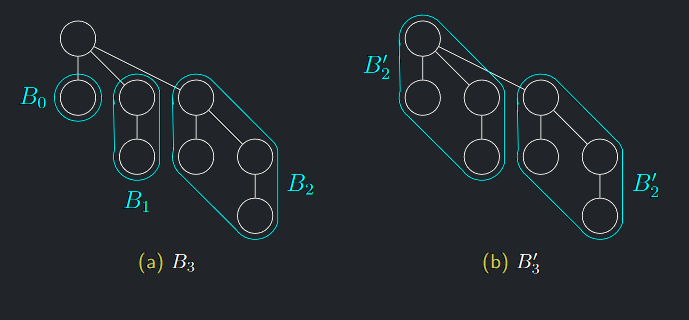
Image title

Důkaz \(B_{k} \implies B^{′}_{k}\)

Matematickou indukcí podle \(k\).
Pro \(k = 0\) tvrzení zjevně platí.
Pod kořenem stromu \(B_{k}\) jsou dle jeho definice zavěšeny stromy \(B_{0}, . . . , B_{k−1}\).
Odtržením nejpravějšího podstromu \(B_{k−1}\) od \(B_{k}\) však dostáváme podle indukčního předpokladu strom \(B_{k−1}\).
To dává přesně definici stromu \(B^{′}_{k}\).

Důkaz \(B^{′}_{k} \implies B_{k}\)

Naopak, uvážíme-li strom \(B^{′}_{k}\), z indukce vyplývá, že \(B^{′}_{k−1}\) je izomorfní s \(B_{k−1}\), pod jehož kořen jsou dle definice napojeny stromy \(B_{0}, . . . , B_{k−2}.\)
Pod kořen \(B^{′}\) k jsou tudíž napojeny stromy \(B_{0}, . . . , B_{k−1}.\)
To dává přesně definici stromu \(B_{k}.\)

Vlastnosti binomiálních stromů

Věta 5.2 (o vlastnostech \(B_{k}\))

Důkaz Věty 5.2

Indukcí podle \(k\).
Strom \(B_{0}\) má jistě \(1\) hladinu a \(2^{0} = 1\) vrchol.
Z indukčního předpokladu vyplývá, že počet hladin \(B_{k−1}\) je \(k\) a počet vrcholů je \(2^{k−1}\).
\(\implies\) vlastnosti \(1\) a \(3\) dokázány.
Užitím dokázané části věty 5.2 dostáváme, že strom \(B_{k}\) je složený ze dvou stromů \(B_{k−1}\), z nichž jeden je o hladinu níže než druhý, což dává počet hladin \(k + 1\) stromu \(B_{k}\).
Složením dvou stromů \(B_{k−1}\) dostáváme \(2 · 2^{k−1} = 2^{k}\) vrcholů.
Stupeň kořene \(B_{k−1}\) je dle IP k − 1 a přidáním jednoho nového syna je stupeň \(B_{k}\) tedy roven \(k\) \(\implies\) vlastnost \(2\) je dokázána

Důsledek

Binomiální strom s \(n\) vrcholy (pokud existuje) má \(1 + log n\) hladin a počet synů kořene \(log n\)

Věta 5.3 (o počtu vrcholů \(B_{k}\) na hladině \(i\))

Počet vrcholů stromu \(B_{k}\) na \(i.\) hladině \((i \in \{0, . . . , k\}) = n_{k}(i) = \binom{k}{i}\)

Důkaz Věty 5.3

Indukcí podle řádu \(k\).
Věta 5.3 platí triviálně pro \(B_{0}\) a \(B_{1}\) (a \(B_{2}\)).
Nechť tedy \(k \geq 2\).
Z definice \(B^{′}_{k}\) plyne, že vrcholy \(B^{′}_{k}\) na \(i.\) hladině, \(0 \lt i \lt k\), jsou tvořeny:
- vrcholy levého \(B^{′}_{k−1}\) na \(i.\) hladině
- vrcholy pravého \(B^{′}_{k−1}\) na \((i − 1).\) hladině.
Z indukčního předpokladu tedy dostaneme Pascalovým pravidlem

\[ n_{k}(i) = n_{k-1}(i) + n_{k-1}(i - 1) = \binom{k-1}{i} + \binom {k-1}{i-1} = \binom{k}{i} \]